Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 100191 by bobhans last updated on 25/Jun/20

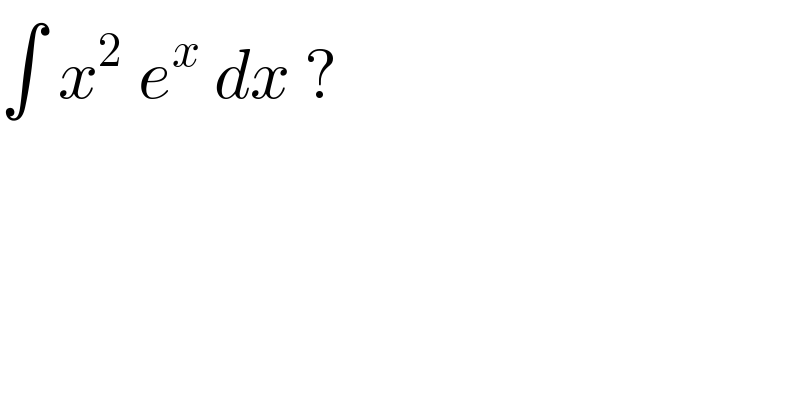
∫ x^2 e^x dx ?

$$\int\:{x}^{\mathrm{2}} \:{e}^{{x}} \:{dx}\:? \\ $$

Commented by bobhans last updated on 25/Jun/20

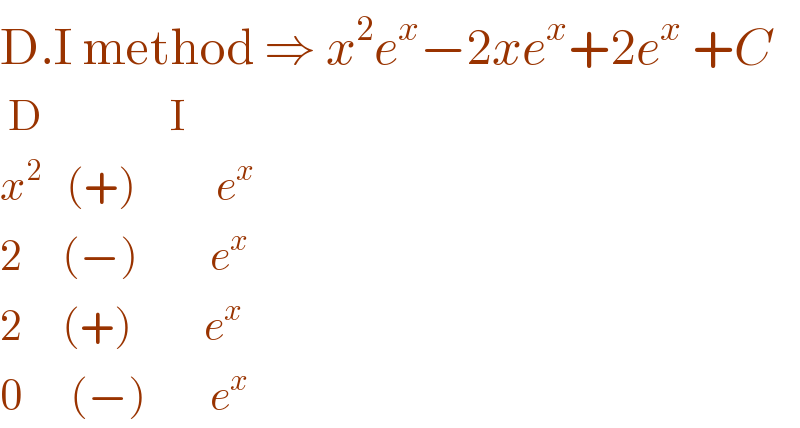
D.I method ⇒ x^2 e^x −2xe^x +2e^x +C D I x^2 (+) e^x 2 (−) e^x 2 (+) e^x 0 (−) e^x

$$\mathrm{D}.\mathrm{I}\:\mathrm{method}\:\Rightarrow\:{x}^{\mathrm{2}} {e}^{{x}} −\mathrm{2}{xe}^{{x}} +\mathrm{2}{e}^{{x}} \:+{C} \\ $$$$\:\mathrm{D}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{I} \\ $$$${x}^{\mathrm{2}} \:\:\:\left(+\right)\:\:\:\:\:\:\:\:\:\:{e}^{{x}} \: \\ $$$$\mathrm{2}\:\:\:\:\:\left(−\right)\:\:\:\:\:\:\:\:\:{e}^{{x}} \\ $$$$\mathrm{2}\:\:\:\:\:\left(+\right)\:\:\:\:\:\:\:\:\:{e}^{{x}} \\ $$$$\mathrm{0}\:\:\:\:\:\:\left(−\right)\:\:\:\:\:\:\:\:{e}^{{x}} \\ $$

Answered by Dwaipayan Shikari last updated on 25/Jun/20

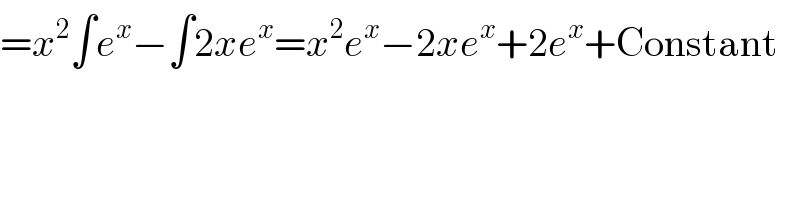
=x^2 ∫e^x −∫2xe^x =x^2 e^x −2xe^x +2e^x +Constant

$$={x}^{\mathrm{2}} \int{e}^{{x}} −\int\mathrm{2}{xe}^{{x}} ={x}^{\mathrm{2}} {e}^{{x}} −\mathrm{2}{xe}^{{x}} +\mathrm{2}{e}^{{x}} +\mathrm{Constant} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com