
Question Number 140751 by peter frank last updated on 12/May/21

Answered by Ar Brandon last updated on 12/May/21
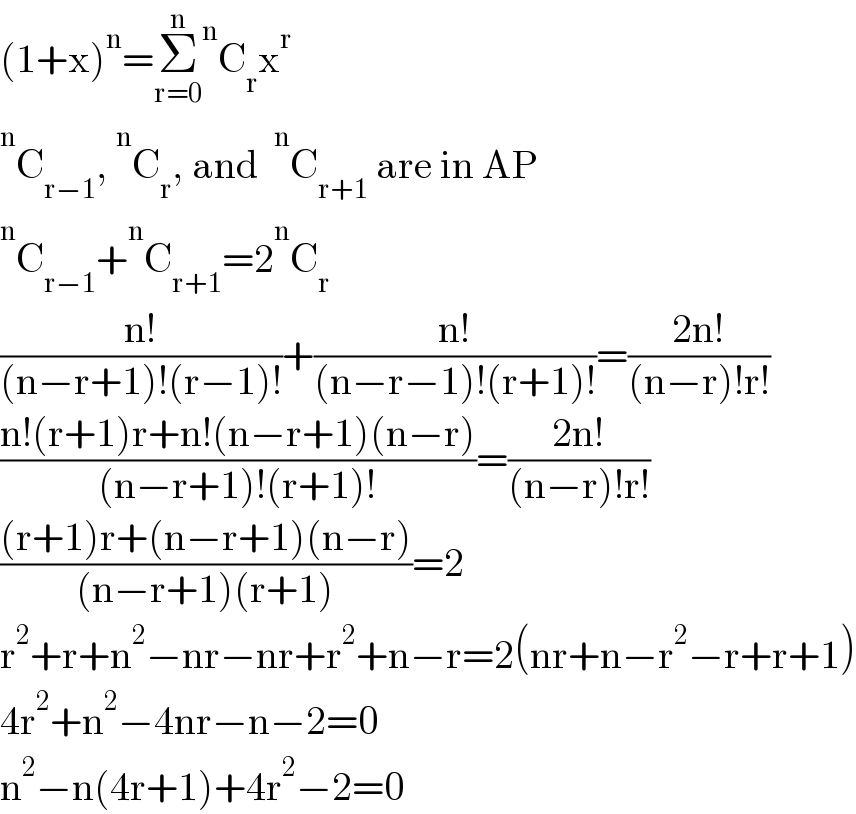
$$\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{n}} =\underset{\mathrm{r}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\overset{\mathrm{n}} {\:}\mathrm{C}_{\mathrm{r}} \mathrm{x}^{\mathrm{r}} \\ $$$$\overset{\mathrm{n}} {\:}\mathrm{C}_{\mathrm{r}−\mathrm{1}} ,\:\overset{\mathrm{n}} {\:}\mathrm{C}_{\mathrm{r}} ,\:\mathrm{and}\:\:\overset{\mathrm{n}} {\:}\mathrm{C}_{\mathrm{r}+\mathrm{1}} \:\mathrm{are}\:\mathrm{in}\:\mathrm{AP} \\ $$$$\overset{\mathrm{n}} {\:}\mathrm{C}_{\mathrm{r}−\mathrm{1}} +\overset{\mathrm{n}} {\:}\mathrm{C}_{\mathrm{r}+\mathrm{1}} =\mathrm{2}\overset{\mathrm{n}} {\:}\mathrm{C}_{\mathrm{r}} \\ $$$$\frac{\mathrm{n}!}{\left(\mathrm{n}−\mathrm{r}+\mathrm{1}\right)!\left(\mathrm{r}−\mathrm{1}\right)!}+\frac{\mathrm{n}!}{\left(\mathrm{n}−\mathrm{r}−\mathrm{1}\right)!\left(\mathrm{r}+\mathrm{1}\right)!}=\frac{\mathrm{2n}!}{\left(\mathrm{n}−\mathrm{r}\right)!\mathrm{r}!} \\ $$$$\frac{\mathrm{n}!\left(\mathrm{r}+\mathrm{1}\right)\mathrm{r}+\mathrm{n}!\left(\mathrm{n}−\mathrm{r}+\mathrm{1}\right)\left(\mathrm{n}−\mathrm{r}\right)}{\left(\mathrm{n}−\mathrm{r}+\mathrm{1}\right)!\left(\mathrm{r}+\mathrm{1}\right)!}=\frac{\mathrm{2n}!}{\left(\mathrm{n}−\mathrm{r}\right)!\mathrm{r}!} \\ $$$$\frac{\left(\mathrm{r}+\mathrm{1}\right)\mathrm{r}+\left(\mathrm{n}−\mathrm{r}+\mathrm{1}\right)\left(\mathrm{n}−\mathrm{r}\right)}{\left(\mathrm{n}−\mathrm{r}+\mathrm{1}\right)\left(\mathrm{r}+\mathrm{1}\right)}=\mathrm{2} \\ $$$$\mathrm{r}^{\mathrm{2}} +\mathrm{r}+\mathrm{n}^{\mathrm{2}} −\mathrm{nr}−\mathrm{nr}+\mathrm{r}^{\mathrm{2}} +\mathrm{n}−\mathrm{r}=\mathrm{2}\left(\mathrm{nr}+\mathrm{n}−\mathrm{r}^{\mathrm{2}} −\mathrm{r}+\mathrm{r}+\mathrm{1}\right) \\ $$$$\mathrm{4r}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} −\mathrm{4nr}−\mathrm{n}−\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{n}^{\mathrm{2}} −\mathrm{n}\left(\mathrm{4r}+\mathrm{1}\right)+\mathrm{4r}^{\mathrm{2}} −\mathrm{2}=\mathrm{0} \\ $$
Commented by peter frank last updated on 12/May/21

$${thank}\:{you} \\ $$
