
Question Number 1407 by 112358 last updated on 29/Jul/15
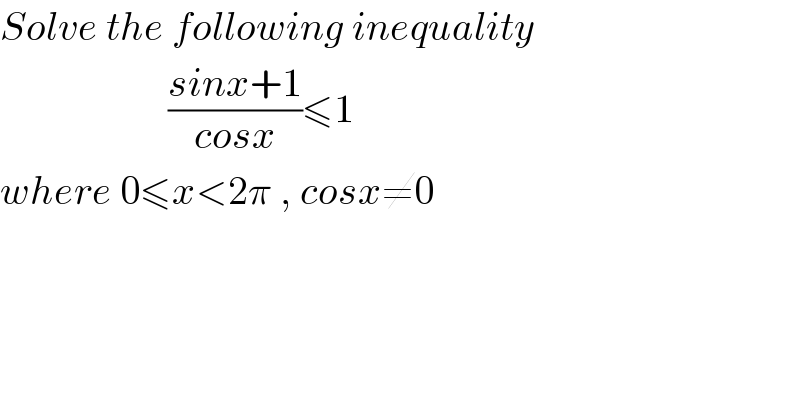
$${Solve}\:{the}\:{following}\:{inequality} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{sinx}+\mathrm{1}}{{cosx}}\leqslant\mathrm{1} \\ $$ $${where}\:\mathrm{0}\leqslant{x}<\mathrm{2}\pi\:,\:{cosx}\neq\mathrm{0} \\ $$
Commented by123456 last updated on 29/Jul/15
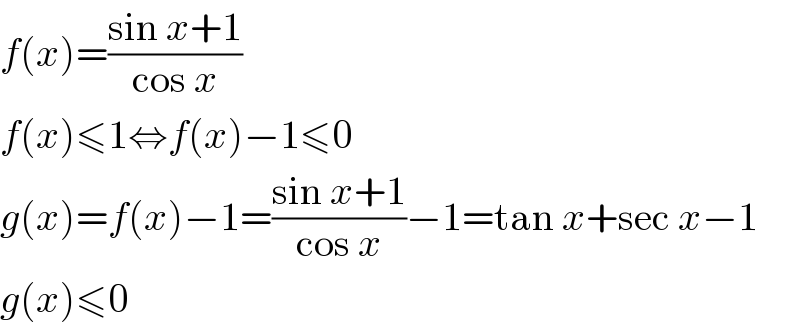
$${f}\left({x}\right)=\frac{\mathrm{sin}\:{x}+\mathrm{1}}{\mathrm{cos}\:{x}} \\ $$ $${f}\left({x}\right)\leqslant\mathrm{1}\Leftrightarrow{f}\left({x}\right)−\mathrm{1}\leqslant\mathrm{0} \\ $$ $${g}\left({x}\right)={f}\left({x}\right)−\mathrm{1}=\frac{\mathrm{sin}\:{x}+\mathrm{1}}{\mathrm{cos}\:{x}}−\mathrm{1}=\mathrm{tan}\:{x}+\mathrm{sec}\:{x}−\mathrm{1} \\ $$ $${g}\left({x}\right)\leqslant\mathrm{0} \\ $$
Commented by112358 last updated on 30/Jul/15
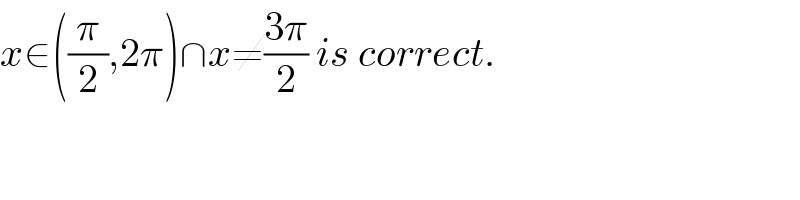
$${x}\in\left(\frac{\pi}{\mathrm{2}},\mathrm{2}\pi\right)\cap{x}\neq\frac{\mathrm{3}\pi}{\mathrm{2}}\:{is}\:{correct}. \\ $$ $$ \\ $$
Commented by123456 last updated on 29/Jul/15
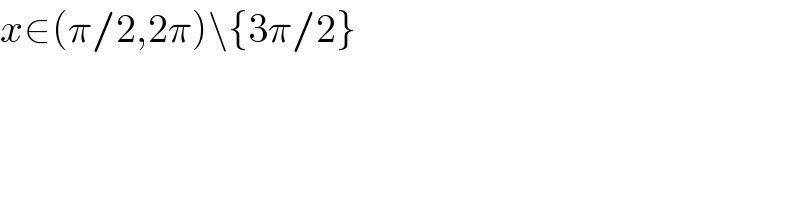
$${x}\in\left(\pi/\mathrm{2},\mathrm{2}\pi\right)\backslash\left\{\mathrm{3}\pi/\mathrm{2}\right\} \\ $$
Commented by112358 last updated on 30/Jul/15

$${Goo}\overset{} {{d}}\:{deduction}! \\ $$
Commented byRasheed Ahmad last updated on 31/Jul/15

$${Sorry}\:{I}\:{accidently}\:{deleted}\:{my}\: \\ $$ $${comment}!\:{There}\:{is}\:{no}\:{way}\:{to}\: \\ $$ $${recover}!\:{I}\:{will}\:{rewrite}\:{it}\:{soon}. \\ $$
Answered by Rasheed Ahmad last updated on 03/Aug/15
![(Rasheed Soomro) Case−I Let x is in Q−I cos x>0 ,sin x>0 ((sin x+1)/(cos x)) ≤1⇒sin x+1 ≤ cos x ⇒sin x ≤ cos x−1 ⇒1≤ −(((1−cos x)/(sin x))) ⇒1 ≤ −tan(x/2)....[∵ ((1−cos x)/(sin x))=tan(x/2)] −1 ≥ tan(x/2) ⇒tan(x/2)≤ −1 (i) But tan(x/2)>0 [(x/2) is in Q−I] (ii) (i) and (ii) are contradictory. They can′t be true simultaneously. Hence in Q−I there is no solution. x ∉ (0,(π/2)) ★★★ Case−II Let x is in Q−II sin x>0 , cos x<0 sin x+1≥ cos x sin x ≥ cos x −1 1 ≥−( ((1−cos x)/(sin x)) ) 1≥ −tan(x/2)⇒−1≤ tan(x/2) tan(x/2) ≥ −1..................(i) Now (x is in Q−II)⇒((x/2) is in Q−I) So, tan(x/2) >0...............(ii) (i) and (ii) have tan(x/2) >0 common for which both are true at same time. So x∈((π/2) , π) ★★★ Case−III Let x is in Q−III sin x < 0 , cos x < 0 Similar way of deduction leads us: tan(x/2) ≤ −1......(i) Now (x is in Q−III)⇒((x/2) is in Q−II) So tan(x/2)<0 .......(ii) Here intersection of (i) and (ii) is tan(x/2) ≤ −1 So the solution of given inequality is ′ solution of tan(x/2) ≤ −1′ tan(x/2) ≤ −1 ⇒ (x/2) ≤ ((3π)/4) ⇒ x ≤((3π)/2) But cos((3π)/2) =0 So finaly x<((3π)/2) This covers whole Q−III x∈(π , ((3π)/2)) ★★★ Case−IV Let x is in Q−IV sin x<0 , cos x>0 In similar way as above we deduce: tan (x/2) ≥ −1..................(i) Now (x is in Q−IV)⇒((x/2) is in Q−II) Hence tan(x/2) < 0...........(ii) (i) and (ii) may be written as: −1≤tan (x/2) <0 tan(x/2) ∈[−1,0) (x/2) ∈[((3π)/4) , π) x ∈[((3π)/2) , 2π) That is whole Q−IV including ((3π)/2) but excuding 2π. But cos((3π)/2)=0 so it also be excluded. Hence x∈(((3π)/2) , 2π) ★★★ Case−V Let x is a quardantal angle For x=(π/2) or ((3π)/2) cos x=0 which is against the restriction cos x≠0. For x=0 or 2π the given inequality holds but 2π is out of domain. Hence only 0 out of quardantal angles is included in solution. Thus, Final Answer is : x ∈{0}∪((π/2) , 2π)−{((3π)/2)}](Q1427.png)
$$\left({Rasheed}\:{Soomro}\right) \\ $$ $${Case}−{I} \\ $$ $${Let}\:{x}\:{is}\:{in}\:{Q}−{I} \\ $$ $${cos}\:{x}>\mathrm{0}\:,{sin}\:{x}>\mathrm{0} \\ $$ $$\frac{{sin}\:{x}+\mathrm{1}}{{cos}\:{x}}\:\leqslant\mathrm{1}\Rightarrow{sin}\:{x}+\mathrm{1}\:\leqslant\:{cos}\:{x} \\ $$ $$\Rightarrow{sin}\:{x}\:\leqslant\:{cos}\:{x}−\mathrm{1} \\ $$ $$\Rightarrow\mathrm{1}\leqslant\:−\left(\frac{\mathrm{1}−{cos}\:{x}}{{sin}\:{x}}\right) \\ $$ $$\Rightarrow\mathrm{1}\:\leqslant\:−{tan}\frac{{x}}{\mathrm{2}}....\left[\because\:\frac{\mathrm{1}−{cos}\:{x}}{{sin}\:{x}}={tan}\frac{{x}}{\mathrm{2}}\right] \\ $$ $$−\mathrm{1}\:\geqslant\:{tan}\frac{{x}}{\mathrm{2}} \\ $$ $$\Rightarrow{tan}\frac{{x}}{\mathrm{2}}\leqslant\:−\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\left({i}\right) \\ $$ $${But}\:{tan}\frac{{x}}{\mathrm{2}}>\mathrm{0}\:\:\:\:\left[\frac{{x}}{\mathrm{2}}\:{is}\:{in}\:{Q}−{I}\right]\:\:\:\left({ii}\right) \\ $$ $$\left({i}\right)\:{and}\:\left({ii}\right)\:{are}\:{contradictory}. \\ $$ $${They}\:{can}'{t}\:{be}\:{true}\:{simultaneously}. \\ $$ $${Hence}\:{in}\:{Q}−{I}\:{there}\:{is}\:{no}\:{solution}. \\ $$ $$\:\:\:\:\:\:\:\:\:{x}\:\notin\:\left(\mathrm{0},\frac{\pi}{\mathrm{2}}\right) \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\bigstar\bigstar\bigstar \\ $$ $${Case}−{II} \\ $$ $${Let}\:{x}\:{is}\:{in}\:{Q}−{II} \\ $$ $${sin}\:{x}>\mathrm{0}\:,\:{cos}\:{x}<\mathrm{0} \\ $$ $${sin}\:{x}+\mathrm{1}\geqslant\:{cos}\:{x}\:\: \\ $$ $${sin}\:{x}\:\geqslant\:{cos}\:{x}\:−\mathrm{1} \\ $$ $$\mathrm{1}\:\geqslant−\left(\:\frac{\mathrm{1}−{cos}\:{x}}{{sin}\:{x}}\:\right) \\ $$ $$\mathrm{1}\geqslant\:−{tan}\frac{{x}}{\mathrm{2}}\Rightarrow−\mathrm{1}\leqslant\:{tan}\frac{{x}}{\mathrm{2}} \\ $$ $${tan}\frac{{x}}{\mathrm{2}}\:\geqslant\:−\mathrm{1}..................\left({i}\right) \\ $$ $${Now}\:\left({x}\:{is}\:{in}\:{Q}−{II}\right)\Rightarrow\left(\frac{{x}}{\mathrm{2}}\:{is}\:{in}\:{Q}−{I}\right) \\ $$ $${So},\:\:{tan}\frac{{x}}{\mathrm{2}}\:>\mathrm{0}...............\left({ii}\right) \\ $$ $$\left({i}\right)\:{and}\:\left({ii}\right)\:{have}\:{tan}\frac{{x}}{\mathrm{2}}\:>\mathrm{0}\:{common}\:{for} \\ $$ $${which}\:{both}\:{are}\:{true}\:{at}\:{same}\:{time}. \\ $$ $${So}\:\boldsymbol{{x}}\in\left(\frac{\pi}{\mathrm{2}}\:,\:\pi\right) \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\bigstar\bigstar\bigstar \\ $$ $${Case}−{III} \\ $$ $${Let}\:{x}\:{is}\:{in}\:{Q}−{III} \\ $$ $${sin}\:{x}\:<\:\mathrm{0}\:,\:{cos}\:{x}\:<\:\mathrm{0} \\ $$ $${Similar}\:{way}\:{of}\:{deduction}\:{leads}\:{us}: \\ $$ $${tan}\frac{{x}}{\mathrm{2}}\:\leqslant\:−\mathrm{1}......\left({i}\right) \\ $$ $${Now} \\ $$ $$\:\:\left({x}\:{is}\:{in}\:{Q}−{III}\right)\Rightarrow\left(\frac{{x}}{\mathrm{2}}\:{is}\:{in}\:{Q}−{II}\right) \\ $$ $${So}\:{tan}\frac{{x}}{\mathrm{2}}<\mathrm{0}\:.......\left({ii}\right) \\ $$ $${Here}\:\:{intersection}\:{of}\:\left({i}\right)\:{and}\:\left({ii}\right) \\ $$ $${is}\:\:\:{tan}\frac{{x}}{\mathrm{2}}\:\leqslant\:−\mathrm{1} \\ $$ $${So}\:{the}\:{solution}\:{of}\:{given}\:{inequality} \\ $$ $${is}\:'\:{solution}\:{of}\:{tan}\frac{{x}}{\mathrm{2}}\:\leqslant\:−\mathrm{1}' \\ $$ $${tan}\frac{{x}}{\mathrm{2}}\:\leqslant\:−\mathrm{1}\:\Rightarrow\:\frac{{x}}{\mathrm{2}}\:\leqslant\:\frac{\mathrm{3}\pi}{\mathrm{4}} \\ $$ $$\Rightarrow\:{x}\:\leqslant\frac{\mathrm{3}\pi}{\mathrm{2}}\: \\ $$ $${But}\:{cos}\frac{\mathrm{3}\pi}{\mathrm{2}}\:=\mathrm{0} \\ $$ $${So}\:{finaly}\:\:{x}<\frac{\mathrm{3}\pi}{\mathrm{2}} \\ $$ $${This}\:{covers}\:{whole}\:{Q}−{III} \\ $$ $$\:\:\:\:\:{x}\in\left(\pi\:,\:\frac{\mathrm{3}\pi}{\mathrm{2}}\right) \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\bigstar\bigstar\bigstar \\ $$ $${Case}−{IV} \\ $$ $${Let}\:{x}\:{is}\:{in}\:{Q}−{IV} \\ $$ $${sin}\:{x}<\mathrm{0}\:,\:{cos}\:{x}>\mathrm{0} \\ $$ $${In}\:{similar}\:{way}\:{as}\:{above}\:{we}\:{deduce}: \\ $$ $${tan}\:\frac{{x}}{\mathrm{2}}\:\geqslant\:−\mathrm{1}..................\left({i}\right) \\ $$ $${Now} \\ $$ $$\left({x}\:{is}\:{in}\:{Q}−{IV}\right)\Rightarrow\left(\frac{{x}}{\mathrm{2}}\:{is}\:{in}\:{Q}−{II}\right) \\ $$ $${Hence}\:{tan}\frac{{x}}{\mathrm{2}}\:<\:\mathrm{0}...........\left({ii}\right) \\ $$ $$\left({i}\right)\:{and}\:\left({ii}\right)\:{may}\:{be}\:{written}\:{as}: \\ $$ $$−\mathrm{1}\leqslant{tan}\:\frac{{x}}{\mathrm{2}}\:<\mathrm{0} \\ $$ $${tan}\frac{{x}}{\mathrm{2}}\:\in\left[−\mathrm{1},\mathrm{0}\right) \\ $$ $$\:\:\:\:\:\frac{{x}}{\mathrm{2}}\:\in\left[\frac{\mathrm{3}\pi}{\mathrm{4}}\:,\:\pi\right) \\ $$ $$\:\:\:\:\:\:\:{x}\:\in\left[\frac{\mathrm{3}\pi}{\mathrm{2}}\:,\:\mathrm{2}\pi\right) \\ $$ $${That}\:{is}\:{whole}\:{Q}−{IV}\:{including} \\ $$ $$\frac{\mathrm{3}\pi}{\mathrm{2}}\:{but}\:{excuding}\:\mathrm{2}\pi. \\ $$ $${But}\:{cos}\frac{\mathrm{3}\pi}{\mathrm{2}}=\mathrm{0}\:{so}\:{it}\:{also}\:{be}\:{excluded}. \\ $$ $${Hence}\:\:\:\:{x}\in\left(\frac{\mathrm{3}\pi}{\mathrm{2}}\:,\:\mathrm{2}\pi\right) \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\bigstar\bigstar\bigstar \\ $$ $${Case}−{V} \\ $$ $${Let}\:{x}\:{is}\:{a}\:{quardantal}\:{angle} \\ $$ $${For}\:{x}=\frac{\pi}{\mathrm{2}}\:{or}\:\frac{\mathrm{3}\pi}{\mathrm{2}}\:{cos}\:{x}=\mathrm{0}\:{which}\:{is} \\ $$ $${against}\:{the}\:{restriction}\:{cos}\:{x}\neq\mathrm{0}. \\ $$ $${For}\:{x}=\mathrm{0}\:{or}\:\mathrm{2}\pi\:{the}\:{given}\:{inequality} \\ $$ $${holds}\:{but}\:\mathrm{2}\pi\:{is}\:{out}\:{of}\:{domain}. \\ $$ $${Hence}\:{only}\:\mathrm{0}\:{out}\:{of}\:{quardantal} \\ $$ $${angles}\:{is}\:{included}\:{in}\:{solution}. \\ $$ $$\boldsymbol{\mathrm{Thus}}, \\ $$ $$\boldsymbol{\mathrm{Final}}\:\boldsymbol{\mathrm{Answer}}\:{is}\:: \\ $$ $${x}\:\in\left\{\mathrm{0}\right\}\cup\left(\frac{\pi}{\mathrm{2}}\:,\:\mathrm{2}\pi\right)−\left\{\frac{\mathrm{3}\pi}{\mathrm{2}}\right\} \\ $$
Commented by123456 last updated on 03/Aug/15

$${f}\left({x}\right)=\frac{\mathrm{sin}\:{x}+\mathrm{1}}{\mathrm{cos}\:{x}} \\ $$ $$\underset{{x}\rightarrow\mathrm{3}\pi/\mathrm{2}} {\mathrm{lim}}\:{f}\left({x}\right)=\mathrm{0}<\mathrm{1} \\ $$ $$\left.\mathrm{this}\:\mathrm{is}\:\mathrm{a}\:\mathrm{curious}\:\mathrm{fact}\::\right) \\ $$
Commented byRasheed Ahmad last updated on 03/Aug/15
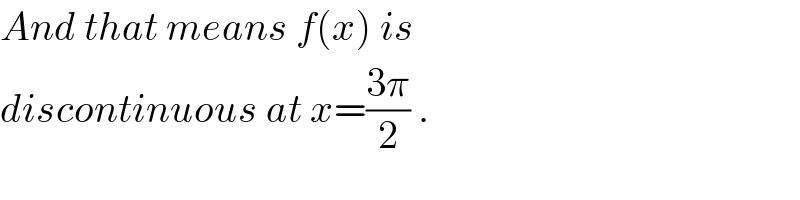
$${And}\:{that}\:{means}\:{f}\left({x}\right)\:{is}\: \\ $$ $${discontinuous}\:{at}\:{x}=\frac{\mathrm{3}\pi}{\mathrm{2}}\:. \\ $$
