
Question Number 96257 by bobhans last updated on 31/May/20
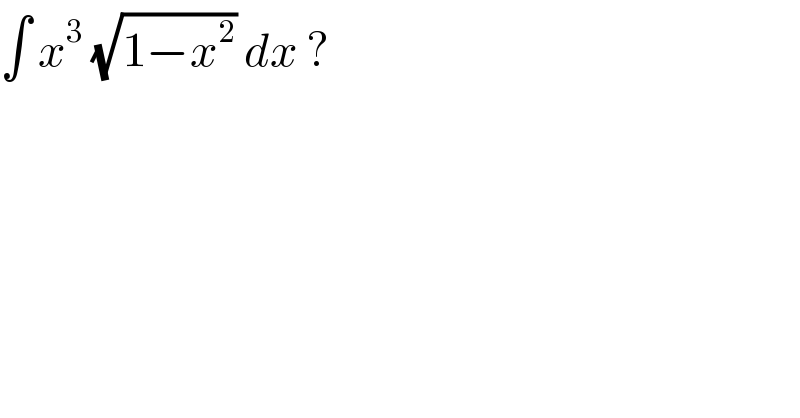
$$\int\:{x}^{\mathrm{3}} \:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:{dx}\:?\: \\ $$
Answered by john santu last updated on 31/May/20
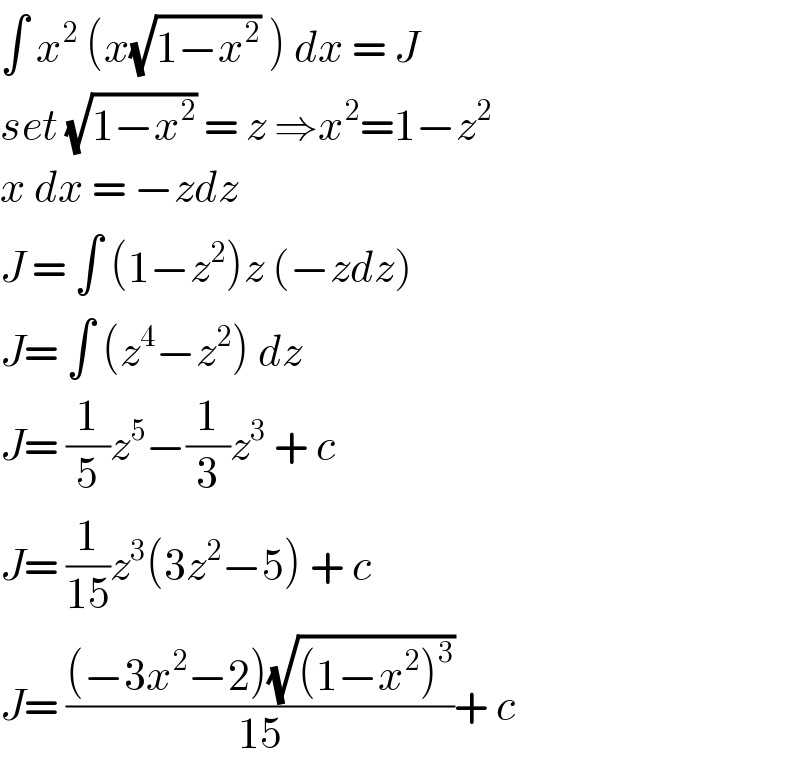
$$\int\:{x}^{\mathrm{2}} \:\left({x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\right)\:{dx}\:=\:{J} \\ $$$${set}\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:=\:{z}\:\Rightarrow{x}^{\mathrm{2}} =\mathrm{1}−{z}^{\mathrm{2}} \\ $$$${x}\:{dx}\:=\:−{zdz}\: \\ $$$${J}\:=\:\int\:\left(\mathrm{1}−{z}^{\mathrm{2}} \right){z}\:\left(−{zdz}\right)\: \\ $$$${J}=\:\int\:\left({z}^{\mathrm{4}} −{z}^{\mathrm{2}} \right)\:{dz}\: \\ $$$${J}=\:\frac{\mathrm{1}}{\mathrm{5}}{z}^{\mathrm{5}} −\frac{\mathrm{1}}{\mathrm{3}}{z}^{\mathrm{3}} \:+\:{c}\: \\ $$$${J}=\:\frac{\mathrm{1}}{\mathrm{15}}{z}^{\mathrm{3}} \left(\mathrm{3}{z}^{\mathrm{2}} −\mathrm{5}\right)\:+\:{c}\: \\ $$$${J}=\:\frac{\left(−\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2}\right)\sqrt{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{3}} }}{\mathrm{15}}+\:{c}\: \\ $$
Commented by bobhans last updated on 31/May/20

$$\mathrm{nice}\:\mathrm{solution}\: \\ $$
