
Question Number 140449 by byaw last updated on 07/May/21

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{first}\:\mathrm{four}\:\mathrm{values}\:\mathrm{of} \\ $$$$\mathrm{2}{x}+\mathrm{5}=\mathrm{1}\left(\mathrm{mod}\:\mathrm{7}\right) \\ $$
Answered by Rasheed.Sindhi last updated on 08/May/21
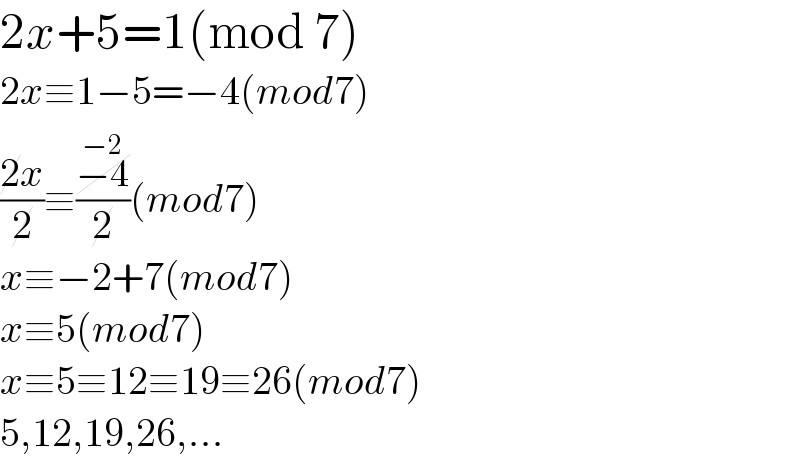
$$\mathrm{2}{x}+\mathrm{5}=\mathrm{1}\left(\mathrm{mod}\:\mathrm{7}\right) \\ $$$$\mathrm{2}{x}\equiv\mathrm{1}−\mathrm{5}=−\mathrm{4}\left({mod}\mathrm{7}\right) \\ $$$$\frac{\cancel{\mathrm{2}}{x}}{\cancel{\mathrm{2}}}\equiv\frac{\cancel{\overset{−\mathrm{2}} {−\mathrm{4}}}}{\cancel{\mathrm{2}}}\left({mod}\mathrm{7}\right) \\ $$$${x}\equiv−\mathrm{2}+\mathrm{7}\left({mod}\mathrm{7}\right) \\ $$$${x}\equiv\mathrm{5}\left({mod}\mathrm{7}\right) \\ $$$${x}\equiv\mathrm{5}\equiv\mathrm{12}\equiv\mathrm{19}\equiv\mathrm{26}\left({mod}\mathrm{7}\right) \\ $$$$\mathrm{5},\mathrm{12},\mathrm{19},\mathrm{26},... \\ $$
