
Question Number 140384 by Willson last updated on 07/May/21
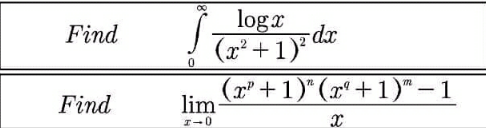
Answered by benjo_mathlover last updated on 07/May/21
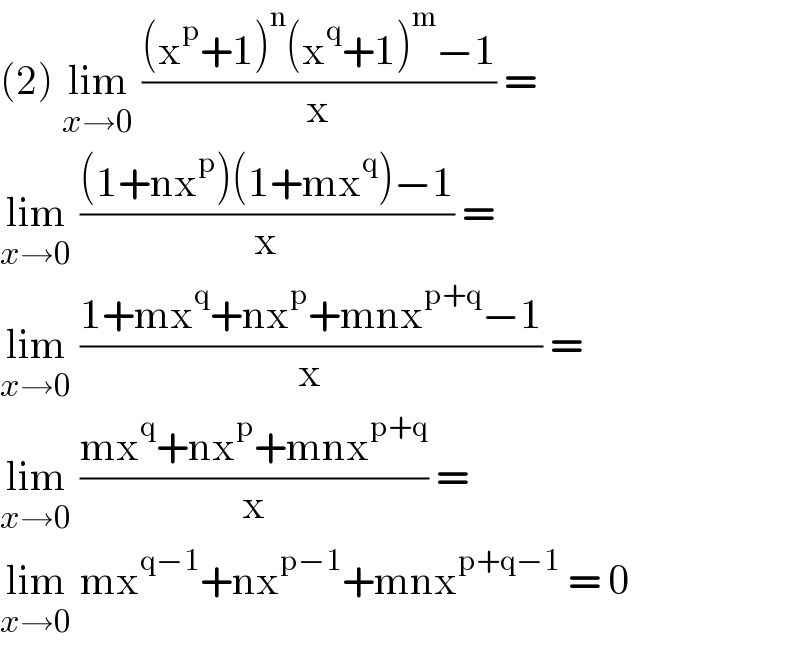
$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{x}^{\mathrm{p}} +\mathrm{1}\right)^{\mathrm{n}} \left(\mathrm{x}^{\mathrm{q}} +\mathrm{1}\right)^{\mathrm{m}} −\mathrm{1}}{\mathrm{x}}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+\mathrm{nx}^{\mathrm{p}} \right)\left(\mathrm{1}+\mathrm{mx}^{\mathrm{q}} \right)−\mathrm{1}}{\mathrm{x}}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}+\mathrm{mx}^{\mathrm{q}} +\mathrm{nx}^{\mathrm{p}} +\mathrm{mnx}^{\mathrm{p}+\mathrm{q}} −\mathrm{1}}{\mathrm{x}}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{mx}^{\mathrm{q}} +\mathrm{nx}^{\mathrm{p}} +\mathrm{mnx}^{\mathrm{p}+\mathrm{q}} }{\mathrm{x}}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{mx}^{\mathrm{q}−\mathrm{1}} +\mathrm{nx}^{\mathrm{p}−\mathrm{1}} +\mathrm{mnx}^{\mathrm{p}+\mathrm{q}−\mathrm{1}} \:=\:\mathrm{0} \\ $$
