
Question Number 140198 by EnterUsername last updated on 05/May/21
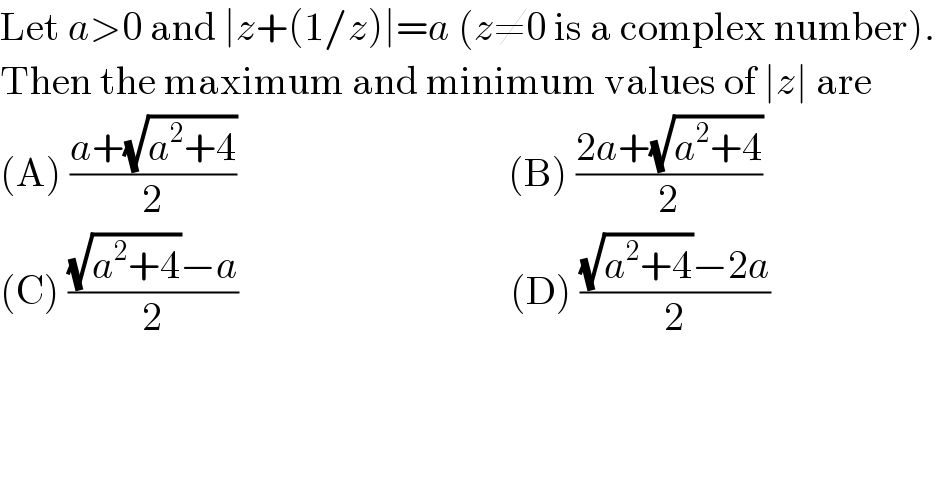
$$\mathrm{Let}\:{a}>\mathrm{0}\:\mathrm{and}\:\mid{z}+\left(\mathrm{1}/{z}\right)\mid={a}\:\left({z}\neq\mathrm{0}\:\mathrm{is}\:\mathrm{a}\:\mathrm{complex}\:\mathrm{number}\right). \\ $$ $$\mathrm{Then}\:\mathrm{the}\:\mathrm{maximum}\:\mathrm{and}\:\mathrm{minimum}\:\mathrm{values}\:\mathrm{of}\:\mid{z}\mid\:\mathrm{are} \\ $$ $$\left(\mathrm{A}\right)\:\frac{{a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{B}\right)\:\frac{\mathrm{2}{a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}} \\ $$ $$\left(\mathrm{C}\right)\:\frac{\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}−{a}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{D}\right)\:\frac{\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}−\mathrm{2}{a}}{\mathrm{2}} \\ $$
Answered by Dwaipayan Shikari last updated on 05/May/21
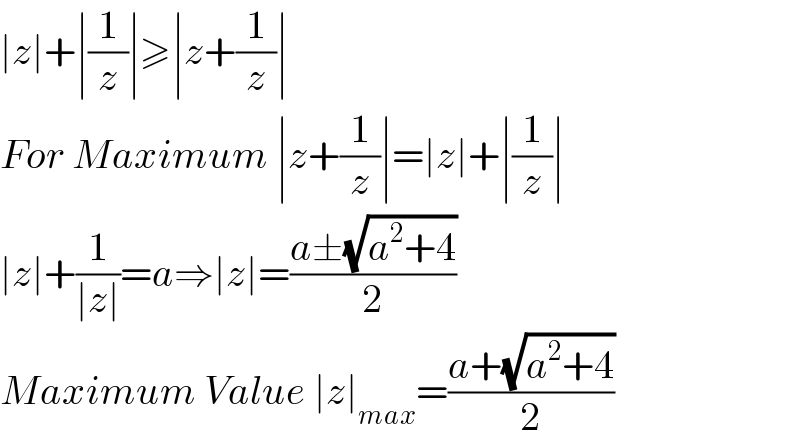
$$\mid{z}\mid+\mid\frac{\mathrm{1}}{{z}}\mid\geqslant\mid{z}+\frac{\mathrm{1}}{{z}}\mid \\ $$ $${For}\:{Maximum}\:\mid{z}+\frac{\mathrm{1}}{{z}}\mid=\mid{z}\mid+\mid\frac{\mathrm{1}}{{z}}\mid \\ $$ $$\mid{z}\mid+\frac{\mathrm{1}}{\mid{z}\mid}={a}\Rightarrow\mid{z}\mid=\frac{{a}\pm\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}} \\ $$ $${Maximum}\:{Value}\:\mid{z}\mid_{{max}} =\frac{{a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}} \\ $$
Commented byEnterUsername last updated on 05/May/21

$$\mathrm{Thanks}\:! \\ $$
Commented bymr W last updated on 05/May/21

$$\mid\frac{\mathrm{1}}{{z}}\mid\neq\frac{\mathrm{1}}{\mid{z}\mid} \\ $$
Answered by mr W last updated on 05/May/21
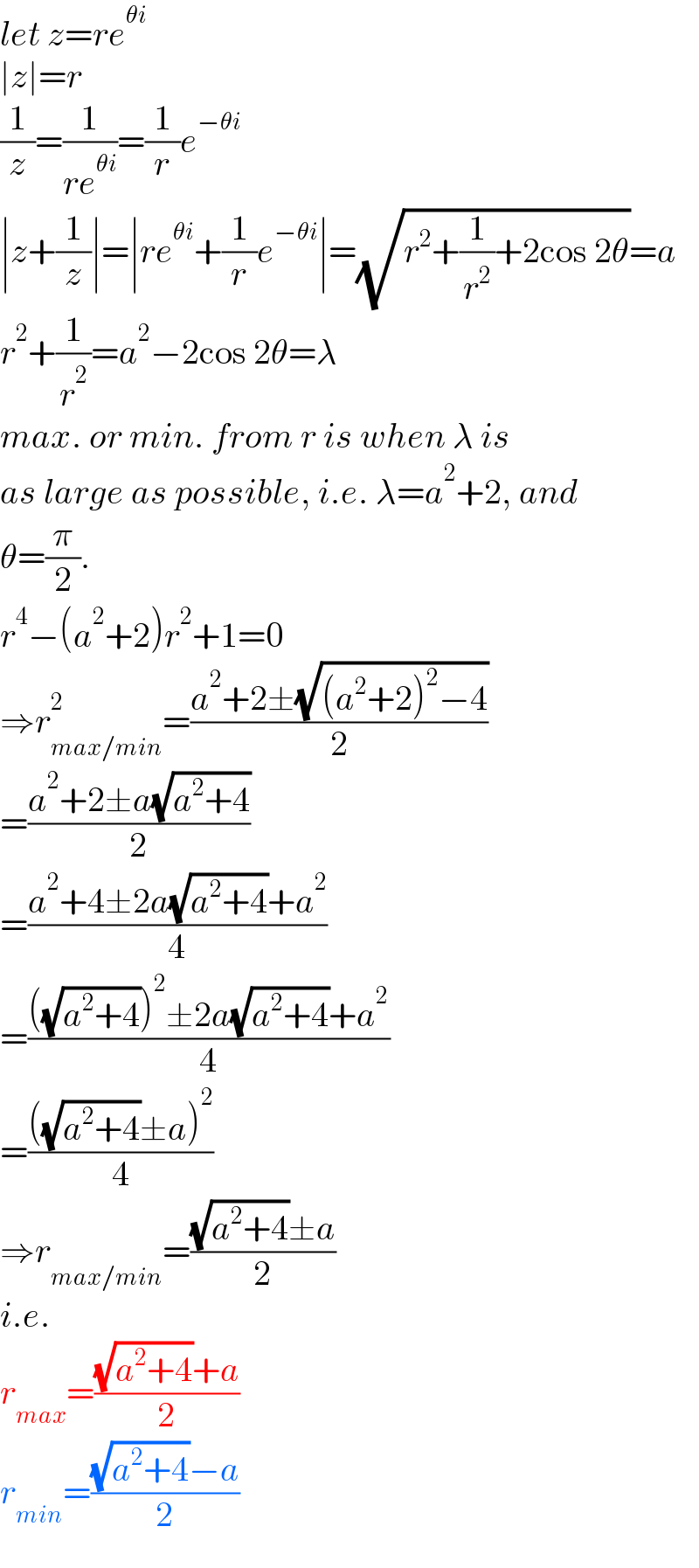
$${let}\:{z}={re}^{\theta{i}} \\ $$ $$\mid{z}\mid={r} \\ $$ $$\frac{\mathrm{1}}{{z}}=\frac{\mathrm{1}}{{re}^{\theta{i}} }=\frac{\mathrm{1}}{{r}}{e}^{−\theta{i}} \\ $$ $$\mid{z}+\frac{\mathrm{1}}{{z}}\mid=\mid{re}^{\theta{i}} +\frac{\mathrm{1}}{{r}}{e}^{−\theta{i}} \mid=\sqrt{{r}^{\mathrm{2}} +\frac{\mathrm{1}}{{r}^{\mathrm{2}} }+\mathrm{2cos}\:\mathrm{2}\theta}={a} \\ $$ $${r}^{\mathrm{2}} +\frac{\mathrm{1}}{{r}^{\mathrm{2}} }={a}^{\mathrm{2}} −\mathrm{2cos}\:\mathrm{2}\theta=\lambda \\ $$ $${max}.\:{or}\:{min}.\:{from}\:{r}\:{is}\:{when}\:\lambda\:{is} \\ $$ $${as}\:{large}\:{as}\:{possible},\:{i}.{e}.\:\lambda={a}^{\mathrm{2}} +\mathrm{2},\:{and} \\ $$ $$\theta=\frac{\pi}{\mathrm{2}}. \\ $$ $${r}^{\mathrm{4}} −\left({a}^{\mathrm{2}} +\mathrm{2}\right){r}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$ $$\Rightarrow{r}_{{max}/{min}} ^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} +\mathrm{2}\pm\sqrt{\left({a}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}} \\ $$ $$=\frac{{a}^{\mathrm{2}} +\mathrm{2}\pm{a}\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}} \\ $$ $$=\frac{{a}^{\mathrm{2}} +\mathrm{4}\pm\mathrm{2}{a}\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}+{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$ $$=\frac{\left(\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}\right)^{\mathrm{2}} \pm\mathrm{2}{a}\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}+{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$ $$=\frac{\left(\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}\pm{a}\right)^{\mathrm{2}} }{\mathrm{4}} \\ $$ $$\Rightarrow{r}_{{max}/{min}} =\frac{\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}\pm{a}}{\mathrm{2}} \\ $$ $${i}.{e}. \\ $$ $${r}_{{max}} =\frac{\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}+{a}}{\mathrm{2}} \\ $$ $${r}_{{min}} =\frac{\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}−{a}}{\mathrm{2}} \\ $$
Commented byEnterUsername last updated on 06/May/21
Thank you Sir
