
Question Number 140113 by EnterUsername last updated on 04/May/21
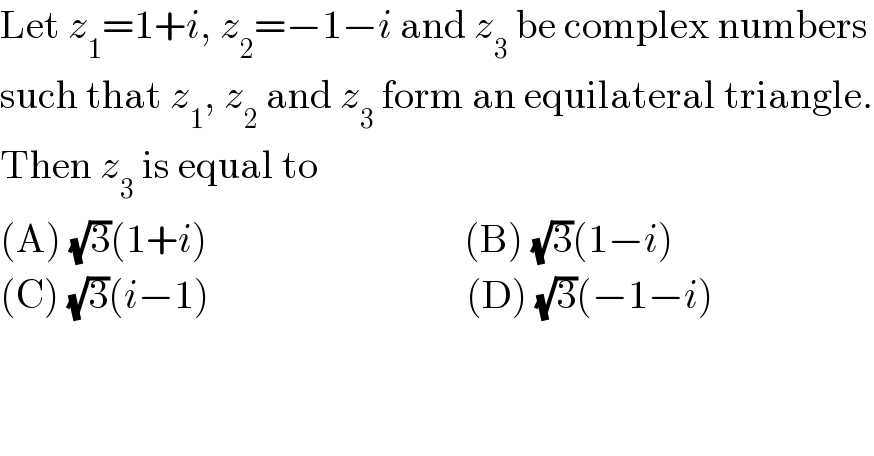
$$\mathrm{Let}\:{z}_{\mathrm{1}} =\mathrm{1}+{i},\:{z}_{\mathrm{2}} =−\mathrm{1}−{i}\:\mathrm{and}\:{z}_{\mathrm{3}} \:\mathrm{be}\:\mathrm{complex}\:\mathrm{numbers} \\ $$$$\mathrm{such}\:\mathrm{that}\:{z}_{\mathrm{1}} ,\:{z}_{\mathrm{2}} \:\mathrm{and}\:{z}_{\mathrm{3}} \:\mathrm{form}\:\mathrm{an}\:\mathrm{equilateral}\:\mathrm{triangle}. \\ $$$$\mathrm{Then}\:{z}_{\mathrm{3}} \:\mathrm{is}\:\mathrm{equal}\:\mathrm{to} \\ $$$$\left(\mathrm{A}\right)\:\sqrt{\mathrm{3}}\left(\mathrm{1}+{i}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{B}\right)\:\sqrt{\mathrm{3}}\left(\mathrm{1}−{i}\right) \\ $$$$\left(\mathrm{C}\right)\:\sqrt{\mathrm{3}}\left({i}−\mathrm{1}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{D}\right)\:\sqrt{\mathrm{3}}\left(−\mathrm{1}−{i}\right) \\ $$
Commented by mr W last updated on 04/May/21
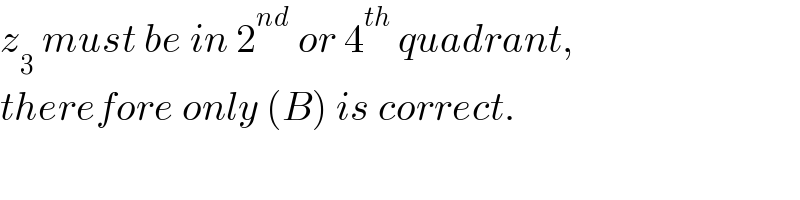
$${z}_{\mathrm{3}} \:{must}\:{be}\:{in}\:\mathrm{2}^{{nd}} \:{or}\:\mathrm{4}^{{th}} \:{quadrant}, \\ $$$${therefore}\:{only}\:\left({B}\right)\:{is}\:{correct}. \\ $$
Commented by EnterUsername last updated on 04/May/21

$$\mathrm{Sir}\:\left(\mathrm{C}\right)\:\mathrm{has}\:\mathrm{also}\:\mathrm{been}\:\mathrm{noted}\:\mathrm{as}\:\mathrm{correct}\:\mathrm{answer}. \\ $$$$\mathrm{How}\:\mathrm{did}\:\mathrm{you}\:\mathrm{get}\:\mathrm{there},\:\mathrm{please}\:? \\ $$
Commented by mr W last updated on 04/May/21
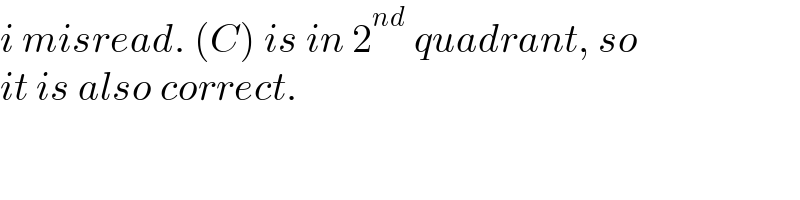
$${i}\:{misread}.\:\left({C}\right)\:{is}\:{in}\:\mathrm{2}^{{nd}} \:{quadrant},\:{so} \\ $$$${it}\:{is}\:{also}\:{correct}. \\ $$
