
Question Number 140055 by mnjuly1970 last updated on 03/May/21
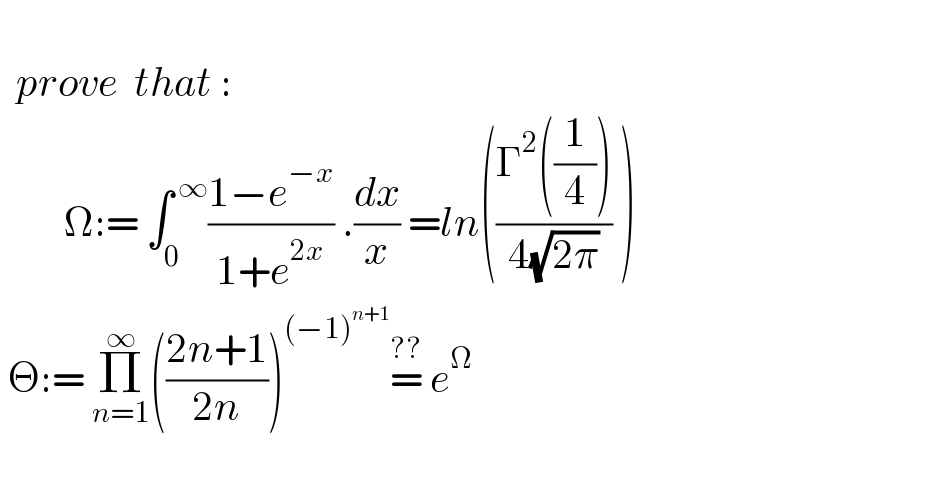
$$\:\:\:\:\:\: \\ $$$$\:\:{prove}\:\:{that}\:: \\ $$$$\:\:\:\:\:\:\:\:\Omega:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{1}−{e}^{−{x}} }{\mathrm{1}+{e}^{\mathrm{2}{x}} }\:.\frac{{dx}}{{x}}\:={ln}\left(\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\mathrm{4}\sqrt{\mathrm{2}\pi}}\:\right) \\ $$$$\:\Theta:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}{n}}\right)^{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} } \overset{??} {=}\:{e}^{\Omega} \\ $$$$\:\:\:\:\:\:\: \\ $$
Answered by Kamel last updated on 03/May/21

Commented by mnjuly1970 last updated on 04/May/21
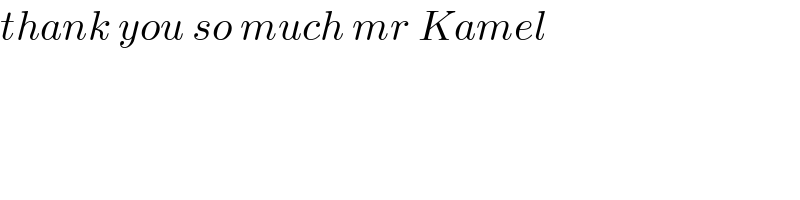
$${thank}\:{you}\:{so}\:{much}\:{mr}\:{Kamel} \\ $$
Answered by Dwaipayan Shikari last updated on 03/May/21
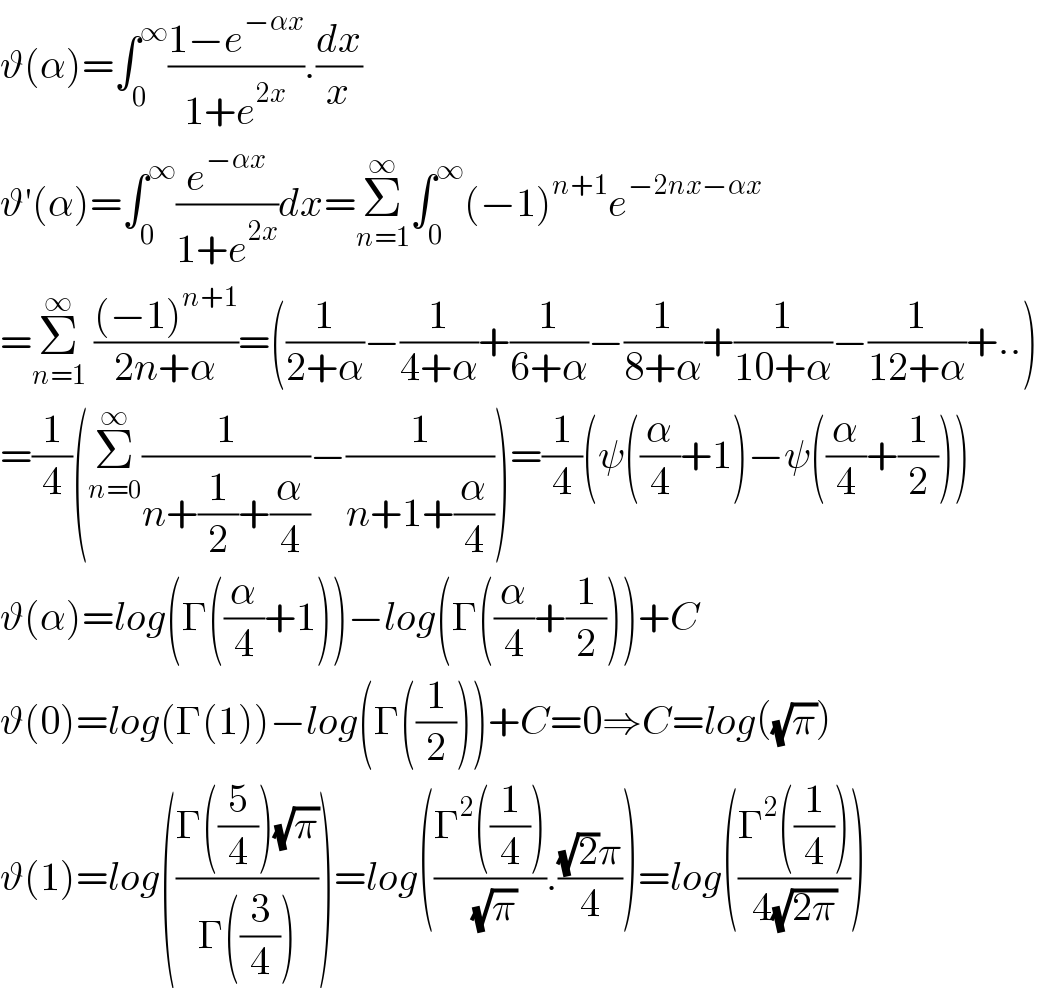
$$\vartheta\left(\alpha\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−{e}^{−\alpha{x}} }{\mathrm{1}+{e}^{\mathrm{2}{x}} }.\frac{{dx}}{{x}} \\ $$$$\vartheta'\left(\alpha\right)=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−\alpha{x}} }{\mathrm{1}+{e}^{\mathrm{2}{x}} }{dx}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {e}^{−\mathrm{2}{nx}−\alpha{x}} \: \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\mathrm{2}{n}+\alpha}=\left(\frac{\mathrm{1}}{\mathrm{2}+\alpha}−\frac{\mathrm{1}}{\mathrm{4}+\alpha}+\frac{\mathrm{1}}{\mathrm{6}+\alpha}−\frac{\mathrm{1}}{\mathrm{8}+\alpha}+\frac{\mathrm{1}}{\mathrm{10}+\alpha}−\frac{\mathrm{1}}{\mathrm{12}+\alpha}+..\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\alpha}{\mathrm{4}}}−\frac{\mathrm{1}}{{n}+\mathrm{1}+\frac{\alpha}{\mathrm{4}}}\right)=\frac{\mathrm{1}}{\mathrm{4}}\left(\psi\left(\frac{\alpha}{\mathrm{4}}+\mathrm{1}\right)−\psi\left(\frac{\alpha}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right) \\ $$$$\vartheta\left(\alpha\right)={log}\left(\Gamma\left(\frac{\alpha}{\mathrm{4}}+\mathrm{1}\right)\right)−{log}\left(\Gamma\left(\frac{\alpha}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right)+{C} \\ $$$$\vartheta\left(\mathrm{0}\right)={log}\left(\Gamma\left(\mathrm{1}\right)\right)−{log}\left(\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)+{C}=\mathrm{0}\Rightarrow{C}={log}\left(\sqrt{\pi}\right) \\ $$$$\vartheta\left(\mathrm{1}\right)={log}\left(\frac{\Gamma\left(\frac{\mathrm{5}}{\mathrm{4}}\right)\sqrt{\pi}}{\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)}\right)={log}\left(\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\:\sqrt{\pi}}.\frac{\sqrt{\mathrm{2}}\pi}{\mathrm{4}}\right)={log}\left(\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\mathrm{4}\sqrt{\mathrm{2}\pi}}\right) \\ $$
Commented by mnjuly1970 last updated on 03/May/21
$$\:\:{zendeh}\:{bashid}\left({be}\:{alive}\right)\:{mr}\:{payan}\:{grateful}.. \\ $$
