
Question Number 139918 by mathsuji last updated on 02/May/21
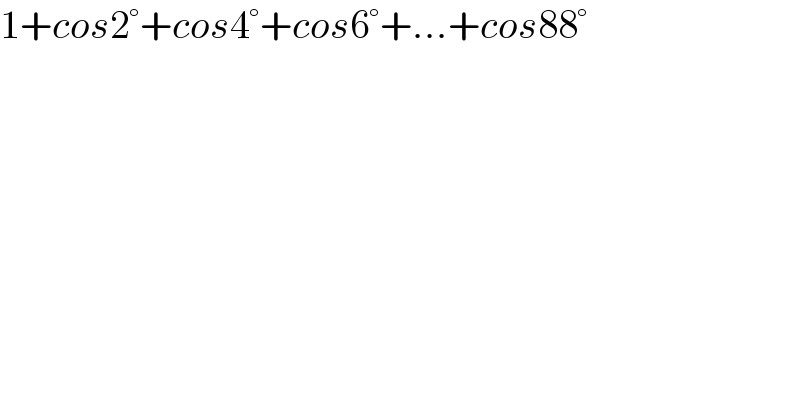
$$\mathrm{1}+{cos}\mathrm{2}°+{cos}\mathrm{4}°+{cos}\mathrm{6}°+...+{cos}\mathrm{88}° \\ $$
Answered by mr W last updated on 02/May/21
![Σ_(k=0) ^(44) (cos ((2kπ)/(180))+i sin ((2kπ)/(180)))=Σ_(k=0) ^(44) e^(((2kπ)/(180))i) =((1−e^(((2πi)/(180))×45) )/(1−e^((2πi)/(180)) ))=((1−i)/((1−cos (π/(90)))−isin (π/(90)))) =(((1−i)[(1−cos (π/(90)))+i sin (π/(90))])/((1−cos (π/(90)))^2 +sin^2 (π/(90)))) =((1−cos (π/(90))+ sin (π/(90))−i(1−cos (π/(90))+sin (π/(90))))/((1−cos (π/(90)))^2 +sin^2 (π/(90)))) =((1−cos (π/(90))+ sin (π/(90))−i(1−cos (π/(90))+sin (π/(90))))/(2(1−cos (π/(90))))) 1+cos 2°+cos 4°+...+cos 88°= =Σ_(k=0) ^(44) cos ((2kπ)/(180)) =((1−cos (π/(90))+ sin (π/(90)))/(2(1−cos (π/(90))))) =(1/2)(1+cot (π/(180))) =(1/2)(1+cot 1°)](Q139934.png)
$$\underset{{k}=\mathrm{0}} {\overset{\mathrm{44}} {\sum}}\left(\mathrm{cos}\:\frac{\mathrm{2}{k}\pi}{\mathrm{180}}+{i}\:\mathrm{sin}\:\frac{\mathrm{2}{k}\pi}{\mathrm{180}}\right)=\underset{{k}=\mathrm{0}} {\overset{\mathrm{44}} {\sum}}{e}^{\frac{\mathrm{2}{k}\pi}{\mathrm{180}}{i}} \\ $$$$=\frac{\mathrm{1}−{e}^{\frac{\mathrm{2}\pi{i}}{\mathrm{180}}×\mathrm{45}} }{\mathrm{1}−{e}^{\frac{\mathrm{2}\pi{i}}{\mathrm{180}}} }=\frac{\mathrm{1}−{i}}{\left(\mathrm{1}−\mathrm{cos}\:\frac{\pi}{\mathrm{90}}\right)−{i}\mathrm{sin}\:\frac{\pi}{\mathrm{90}}} \\ $$$$=\frac{\left(\mathrm{1}−{i}\right)\left[\left(\mathrm{1}−\mathrm{cos}\:\frac{\pi}{\mathrm{90}}\right)+{i}\:\mathrm{sin}\:\frac{\pi}{\mathrm{90}}\right]}{\left(\mathrm{1}−\mathrm{cos}\:\frac{\pi}{\mathrm{90}}\right)^{\mathrm{2}} +\mathrm{sin}^{\mathrm{2}} \:\frac{\pi}{\mathrm{90}}} \\ $$$$=\frac{\mathrm{1}−\mathrm{cos}\:\frac{\pi}{\mathrm{90}}+\:\mathrm{sin}\:\frac{\pi}{\mathrm{90}}−{i}\left(\mathrm{1}−\mathrm{cos}\:\frac{\pi}{\mathrm{90}}+\mathrm{sin}\:\frac{\pi}{\mathrm{90}}\right)}{\left(\mathrm{1}−\mathrm{cos}\:\frac{\pi}{\mathrm{90}}\right)^{\mathrm{2}} +\mathrm{sin}^{\mathrm{2}} \:\frac{\pi}{\mathrm{90}}} \\ $$$$=\frac{\mathrm{1}−\mathrm{cos}\:\frac{\pi}{\mathrm{90}}+\:\mathrm{sin}\:\frac{\pi}{\mathrm{90}}−{i}\left(\mathrm{1}−\mathrm{cos}\:\frac{\pi}{\mathrm{90}}+\mathrm{sin}\:\frac{\pi}{\mathrm{90}}\right)}{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\frac{\pi}{\mathrm{90}}\right)} \\ $$$$ \\ $$$$\mathrm{1}+\mathrm{cos}\:\mathrm{2}°+\mathrm{cos}\:\mathrm{4}°+...+\mathrm{cos}\:\mathrm{88}°= \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{\mathrm{44}} {\sum}}\mathrm{cos}\:\frac{\mathrm{2}{k}\pi}{\mathrm{180}} \\ $$$$=\frac{\mathrm{1}−\mathrm{cos}\:\frac{\pi}{\mathrm{90}}+\:\mathrm{sin}\:\frac{\pi}{\mathrm{90}}}{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\frac{\pi}{\mathrm{90}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{cot}\:\frac{\pi}{\mathrm{180}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{cot}\:\mathrm{1}°\right) \\ $$
Commented by mathsuji last updated on 02/May/21
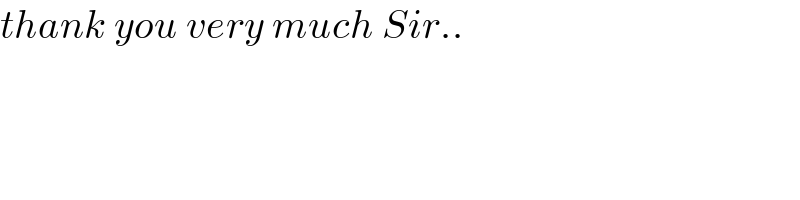
$${thank}\:{you}\:{very}\:{much}\:{Sir}.. \\ $$
