
Question Number 139911 by mathdanisur last updated on 02/May/21
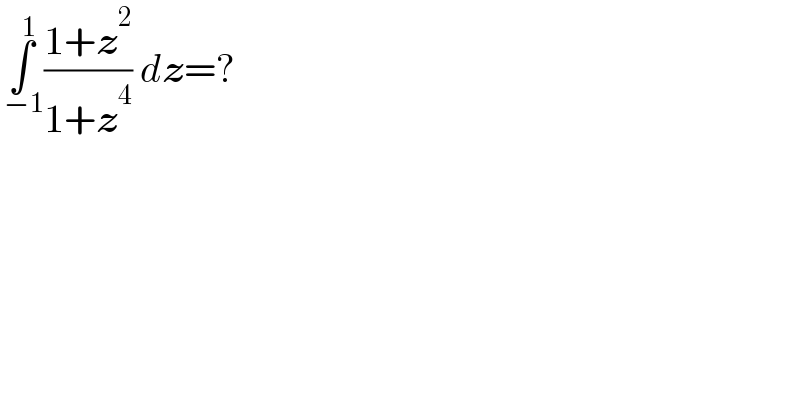
$$\underset{\:−\mathrm{1}} {\overset{\:\mathrm{1}} {\int}}\frac{\mathrm{1}+\boldsymbol{{z}}^{\mathrm{2}} }{\mathrm{1}+\boldsymbol{{z}}^{\mathrm{4}} }\:{d}\boldsymbol{{z}}=? \\ $$
Answered by Dwaipayan Shikari last updated on 02/May/21
![∫_(−1) ^1 ((1+z^2 )/(1+z^4 ))dz =(1/2)∫_(−1) ^1 (1/((z^2 −(√2)z+1)))+(1/((z^2 +(√2)z+1)))dz =∫_0 ^1 (1/(z^2 −(√2)z+1 ))+(1/(z^2 +(√2)z+1))dz =[(√2)tan^(−1) ((√2)z−1)]_0 ^1 +[(√2)tan^(−1) ((√2)z+1)]_0 ^1 =(√2) tan^(−1) ((√2)−1)+(√2) tan^(−1) ((√2)+1) =(√2) tan^(−1) (((√2)−1+(√2)+1)/(1−(2−1)))=(√2) .(π/2)=(π/( (√2)))](Q139915.png)
$$\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{\mathrm{1}+{z}^{\mathrm{2}} }{\mathrm{1}+{z}^{\mathrm{4}} }{dz} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{\mathrm{1}}{\left({z}^{\mathrm{2}} −\sqrt{\mathrm{2}}{z}+\mathrm{1}\right)}+\frac{\mathrm{1}}{\left({z}^{\mathrm{2}} +\sqrt{\mathrm{2}}{z}+\mathrm{1}\right)}{dz} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{z}^{\mathrm{2}} −\sqrt{\mathrm{2}}{z}+\mathrm{1}\:}+\frac{\mathrm{1}}{{z}^{\mathrm{2}} +\sqrt{\mathrm{2}}{z}+\mathrm{1}}{dz}\:\:\:\:\:\:\: \\ $$$$=\left[\sqrt{\mathrm{2}}{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}}{z}−\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} +\left[\sqrt{\mathrm{2}}{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}}{z}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\sqrt{\mathrm{2}}\:{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}}−\mathrm{1}\right)+\sqrt{\mathrm{2}}\:{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}}+\mathrm{1}\right) \\ $$$$=\sqrt{\mathrm{2}}\:{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{2}}−\mathrm{1}+\sqrt{\mathrm{2}}+\mathrm{1}}{\mathrm{1}−\left(\mathrm{2}−\mathrm{1}\right)}=\sqrt{\mathrm{2}}\:.\frac{\pi}{\mathrm{2}}=\frac{\pi}{\:\sqrt{\mathrm{2}}} \\ $$
Commented by mathdanisur last updated on 02/May/21
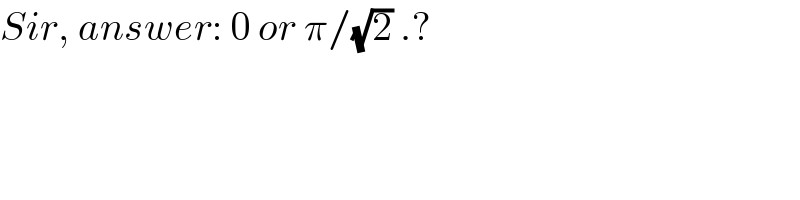
$${Sir},\:{answer}:\:\mathrm{0}\:{or}\:\pi/\sqrt{\mathrm{2}}\:.? \\ $$
Commented by Dwaipayan Shikari last updated on 02/May/21
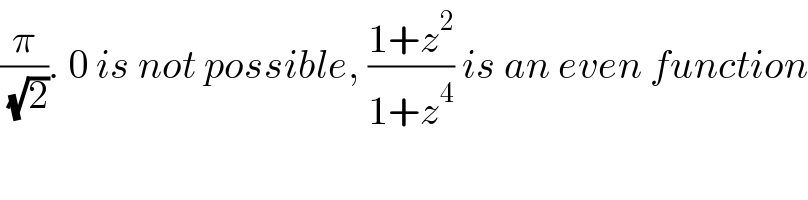
$$\frac{\pi}{\:\sqrt{\mathrm{2}}}.\:\mathrm{0}\:{is}\:{not}\:{possible},\:\frac{\mathrm{1}+{z}^{\mathrm{2}} }{\mathrm{1}+{z}^{\mathrm{4}} }\:{is}\:{an}\:{even}\:{function} \\ $$
Commented by MJS_new last updated on 02/May/21
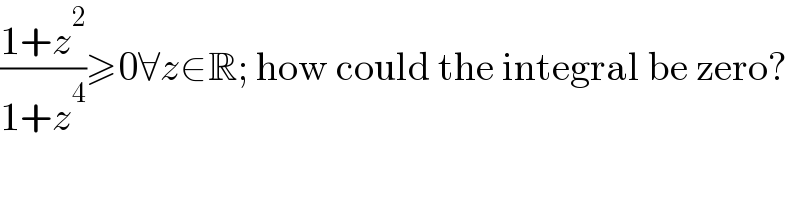
$$\frac{\mathrm{1}+{z}^{\mathrm{2}} }{\mathrm{1}+{z}^{\mathrm{4}} }\geqslant\mathrm{0}\forall{z}\in\mathbb{R};\:\mathrm{how}\:\mathrm{could}\:\mathrm{the}\:\mathrm{integral}\:\mathrm{be}\:\mathrm{zero}? \\ $$
Commented by mathdanisur last updated on 02/May/21

$${thanks}\:{Sir} \\ $$
Answered by Mathspace last updated on 02/May/21
![I=∫_(−1) ^1 ((1+(1/z^2 ))/(z^2 +(1/z^2 )))dz =2∫_0 ^1 ((1+(1/z^2 ))/((z−(1/z))^2 +2))dz =_(z−(1/z)=−t) 2 ∫_∞ ^0 ((−dt)/(t^2 +2)) =2∫_0 ^∞ (dt/(t^2 +2)) =_(t=.(√2)y) 2∫_0 ^∞ (((√2)dy)/(2(1+y^2 ))) =(√2).[arctany]_0 ^∞ =((π(√2))/2)](Q139923.png)
$${I}=\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{\mathrm{1}+\frac{\mathrm{1}}{{z}^{\mathrm{2}} }}{{z}^{\mathrm{2}} +\frac{\mathrm{1}}{{z}^{\mathrm{2}} }}{dz} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}+\frac{\mathrm{1}}{{z}^{\mathrm{2}} }}{\left({z}−\frac{\mathrm{1}}{{z}}\right)^{\mathrm{2}} +\mathrm{2}}{dz} \\ $$$$=_{{z}−\frac{\mathrm{1}}{{z}}=−{t}} \:\mathrm{2}\:\int_{\infty} ^{\mathrm{0}} \:\:\frac{−{dt}}{{t}^{\mathrm{2}} +\mathrm{2}} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{2}}\:=_{{t}=.\sqrt{\mathrm{2}}{y}} \:\:\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\sqrt{\mathrm{2}}{dy}}{\mathrm{2}\left(\mathrm{1}+{y}^{\mathrm{2}} \right)} \\ $$$$=\sqrt{\mathrm{2}}.\left[{arctany}\right]_{\mathrm{0}} ^{\infty} \:=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$
Commented by mathdanisur last updated on 02/May/21

$${thank}\:{you}\:{Sir} \\ $$
