
Question Number 139878 by bramlexs22 last updated on 02/May/21
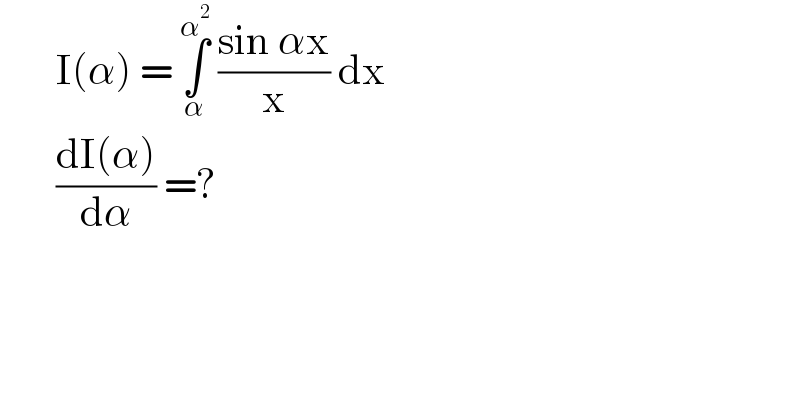
$$\:\:\:\:\:\:\:\mathrm{I}\left(\alpha\right)\:=\:\underset{\alpha} {\overset{\alpha^{\mathrm{2}} } {\int}}\:\frac{\mathrm{sin}\:\alpha\mathrm{x}}{\mathrm{x}}\:\mathrm{dx}\: \\ $$$$\:\:\:\:\:\:\:\frac{\mathrm{dI}\left(\alpha\right)}{\mathrm{d}\alpha}\:=? \\ $$
Answered by EDWIN88 last updated on 02/May/21
![(dI/dα) = ∫_α ^α^2 (∂/∂α)(((sin αx)/x)) dx + ((sin α^3 )/α^2 )(2α)−((sin α^2 )/α)(1) = ∫_α ^α^2 cos αx dx + ((2sin α^3 −sin α^2 )/α) = [ (1/α)sin αx ]_α ^α^2 + ((2sin α^3 −sin α^2 )/α) = ((sin α^3 −sin α^2 )/α)+((2sin α^3 −sin α^2 )/α) = ((3sin α^3 −2sin α^2 )/α)](Q139879.png)
$$\:\:\:\:\:\frac{\mathrm{dI}}{\mathrm{d}\alpha}\:=\:\underset{\alpha} {\overset{\alpha^{\mathrm{2}} } {\int}}\:\frac{\partial}{\partial\alpha}\left(\frac{\mathrm{sin}\:\alpha\mathrm{x}}{\mathrm{x}}\right)\:\mathrm{dx}\:+\:\frac{\mathrm{sin}\:\alpha^{\mathrm{3}} }{\alpha^{\mathrm{2}} }\left(\mathrm{2}\alpha\right)−\frac{\mathrm{sin}\:\alpha^{\mathrm{2}} }{\alpha}\left(\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\underset{\alpha} {\overset{\alpha^{\mathrm{2}} } {\int}}\:\mathrm{cos}\:\alpha\mathrm{x}\:\mathrm{dx}\:+\:\frac{\mathrm{2sin}\:\alpha^{\mathrm{3}} −\mathrm{sin}\:\alpha^{\mathrm{2}} }{\alpha} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\left[\:\frac{\mathrm{1}}{\alpha}\mathrm{sin}\:\alpha\mathrm{x}\:\right]_{\alpha} ^{\alpha^{\mathrm{2}} } +\:\frac{\mathrm{2sin}\:\alpha^{\mathrm{3}} −\mathrm{sin}\:\alpha^{\mathrm{2}} }{\alpha} \\ $$$$\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{sin}\:\alpha^{\mathrm{3}} −\mathrm{sin}\:\alpha^{\mathrm{2}} }{\alpha}+\frac{\mathrm{2sin}\:\alpha^{\mathrm{3}} −\mathrm{sin}\:\alpha^{\mathrm{2}} }{\alpha} \\ $$$$\:\:\:\:\:\:\:\:=\:\frac{\mathrm{3sin}\:\alpha^{\mathrm{3}} −\mathrm{2sin}\:\alpha^{\mathrm{2}} }{\alpha} \\ $$
Answered by mathmax by abdo last updated on 02/May/21
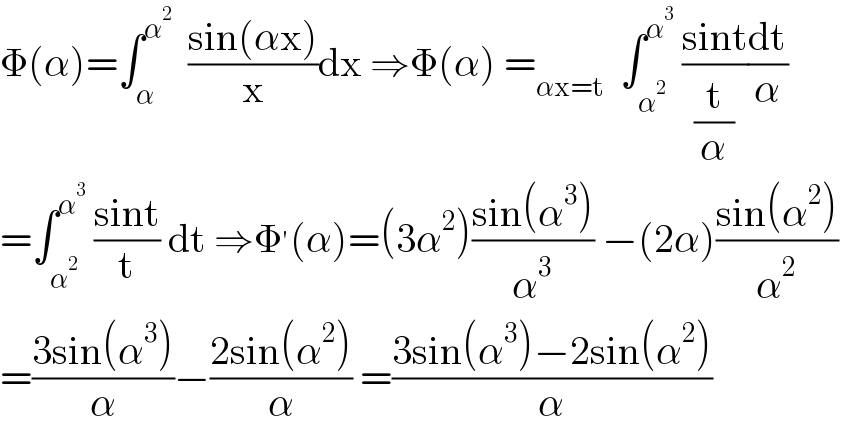
$$\Phi\left(\alpha\right)=\int_{\alpha} ^{\alpha^{\mathrm{2}} } \:\:\frac{\mathrm{sin}\left(\alpha\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}\:\Rightarrow\Phi\left(\alpha\right)\:=_{\alpha\mathrm{x}=\mathrm{t}} \:\:\int_{\alpha^{\mathrm{2}} } ^{\alpha^{\mathrm{3}} } \:\frac{\mathrm{sint}}{\frac{\mathrm{t}}{\alpha}}\frac{\mathrm{dt}}{\alpha} \\ $$$$=\int_{\alpha^{\mathrm{2}} } ^{\alpha^{\mathrm{3}} } \:\frac{\mathrm{sint}}{\mathrm{t}}\:\mathrm{dt}\:\Rightarrow\Phi^{'} \left(\alpha\right)=\left(\mathrm{3}\alpha^{\mathrm{2}} \right)\frac{\mathrm{sin}\left(\alpha^{\mathrm{3}} \right)}{\alpha^{\mathrm{3}} }\:−\left(\mathrm{2}\alpha\right)\frac{\mathrm{sin}\left(\alpha^{\mathrm{2}} \right)}{\alpha^{\mathrm{2}} }\: \\ $$$$=\frac{\mathrm{3sin}\left(\alpha^{\mathrm{3}} \right)}{\alpha}−\frac{\mathrm{2sin}\left(\alpha^{\mathrm{2}} \right)}{\alpha}\:=\frac{\mathrm{3sin}\left(\alpha^{\mathrm{3}} \right)−\mathrm{2sin}\left(\alpha^{\mathrm{2}} \right)}{\alpha} \\ $$
