
Previous in Probability and Statistics Next in Probability and Statistics
Question Number 139868 by I want to learn more last updated on 01/May/21

Answered by TheSupreme last updated on 02/May/21
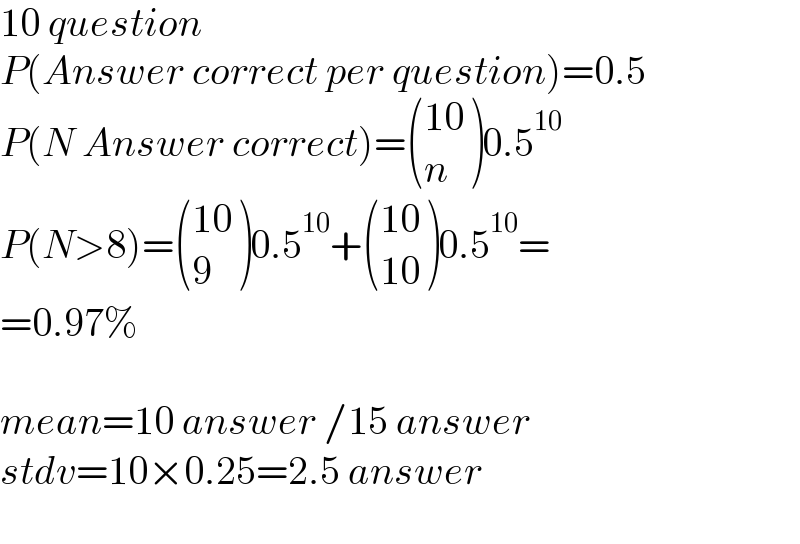
$$\mathrm{10}\:{question} \\ $$$${P}\left({Answer}\:{correct}\:{per}\:{question}\right)=\mathrm{0}.\mathrm{5} \\ $$$${P}\left({N}\:{Answer}\:{correct}\right)=\begin{pmatrix}{\mathrm{10}}\\{{n}}\end{pmatrix}\mathrm{0}.\mathrm{5}^{\mathrm{10}} \\ $$$${P}\left({N}>\mathrm{8}\right)=\begin{pmatrix}{\mathrm{10}}\\{\mathrm{9}}\end{pmatrix}\mathrm{0}.\mathrm{5}^{\mathrm{10}} +\begin{pmatrix}{\mathrm{10}}\\{\mathrm{10}}\end{pmatrix}\mathrm{0}.\mathrm{5}^{\mathrm{10}} = \\ $$$$=\mathrm{0}.\mathrm{97\%} \\ $$$$ \\ $$$${mean}=\mathrm{10}\:{answer}\:/\mathrm{15}\:{answer} \\ $$$${stdv}=\mathrm{10}×\mathrm{0}.\mathrm{25}=\mathrm{2}.\mathrm{5}\:{answer}\: \\ $$$$ \\ $$
Commented by I want to learn more last updated on 02/May/21
$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
Commented by mr W last updated on 02/May/21

$$\frac{\mathrm{11}}{\mathrm{1024}}\approx\mathrm{1}.\mathrm{07\%} \\ $$
Commented by I want to learn more last updated on 02/May/21

$$\mathrm{Sir},\:\mathrm{please}\:\mathrm{full}\:\mathrm{workings}\:\mathrm{please}. \\ $$
Commented by mr W last updated on 02/May/21
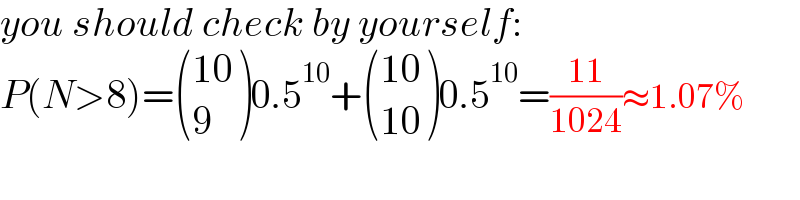
$${you}\:{should}\:{check}\:{by}\:{yourself}: \\ $$$${P}\left({N}>\mathrm{8}\right)=\begin{pmatrix}{\mathrm{10}}\\{\mathrm{9}}\end{pmatrix}\mathrm{0}.\mathrm{5}^{\mathrm{10}} +\begin{pmatrix}{\mathrm{10}}\\{\mathrm{10}}\end{pmatrix}\mathrm{0}.\mathrm{5}^{\mathrm{10}} =\frac{\mathrm{11}}{\mathrm{1024}}\approx\mathrm{1}.\mathrm{07\%} \\ $$
Answered by mr W last updated on 02/May/21

$$\mathrm{10}\:{questions}\: \\ $$$${totally}\:\mathrm{2}^{\mathrm{10}} =\mathrm{1024}\:{possibilities} \\ $$$$\mathrm{9}\:{questions}\:{are}\:{correct}\:{means}\:{one} \\ $$$${question}\:{is}\:{wrong}:\:\mathrm{10}\:{possibility} \\ $$$$\mathrm{10}\:{questions}\:{are}\:{correct}:\:\mathrm{1}\:{possibility} \\ $$$${p}=\frac{\mathrm{10}+\mathrm{1}}{\mathrm{2}^{\mathrm{10}} }=\frac{\mathrm{11}}{\mathrm{1024}}\approx\mathrm{1}.\mathrm{07\%} \\ $$
