
Question Number 139867 by Maclaurin Stickker last updated on 01/May/21
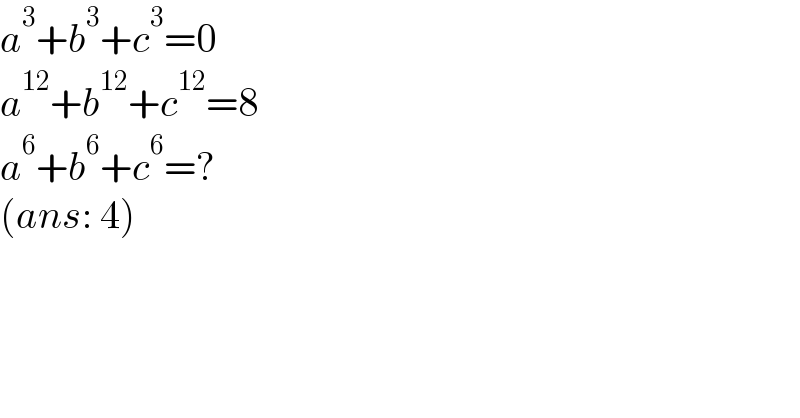
$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} =\mathrm{0} \\ $$$${a}^{\mathrm{12}} +{b}^{\mathrm{12}} +{c}^{\mathrm{12}} =\mathrm{8} \\ $$$${a}^{\mathrm{6}} +{b}^{\mathrm{6}} +{c}^{\mathrm{6}} =? \\ $$$$\left({ans}:\:\mathrm{4}\right) \\ $$$$ \\ $$
Answered by MJS_new last updated on 02/May/21
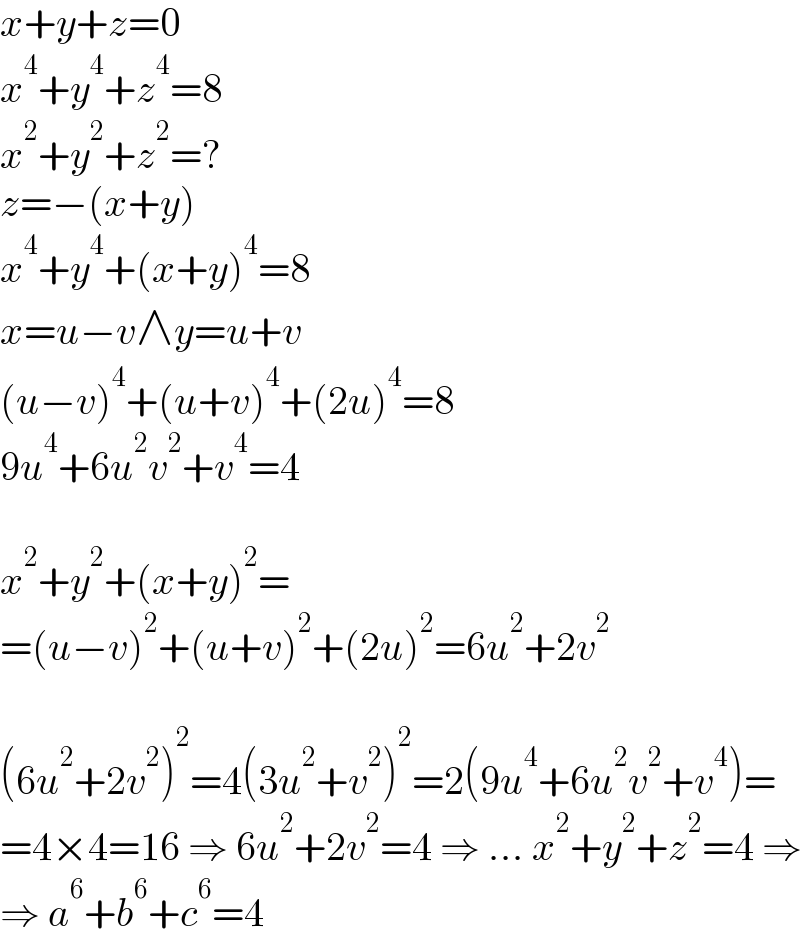
$${x}+{y}+{z}=\mathrm{0} \\ $$$${x}^{\mathrm{4}} +{y}^{\mathrm{4}} +{z}^{\mathrm{4}} =\mathrm{8} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} =? \\ $$$${z}=−\left({x}+{y}\right) \\ $$$${x}^{\mathrm{4}} +{y}^{\mathrm{4}} +\left({x}+{y}\right)^{\mathrm{4}} =\mathrm{8} \\ $$$${x}={u}−{v}\wedge{y}={u}+{v} \\ $$$$\left({u}−{v}\right)^{\mathrm{4}} +\left({u}+{v}\right)^{\mathrm{4}} +\left(\mathrm{2}{u}\right)^{\mathrm{4}} =\mathrm{8} \\ $$$$\mathrm{9}{u}^{\mathrm{4}} +\mathrm{6}{u}^{\mathrm{2}} {v}^{\mathrm{2}} +{v}^{\mathrm{4}} =\mathrm{4} \\ $$$$ \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\left({x}+{y}\right)^{\mathrm{2}} = \\ $$$$=\left({u}−{v}\right)^{\mathrm{2}} +\left({u}+{v}\right)^{\mathrm{2}} +\left(\mathrm{2}{u}\right)^{\mathrm{2}} =\mathrm{6}{u}^{\mathrm{2}} +\mathrm{2}{v}^{\mathrm{2}} \\ $$$$ \\ $$$$\left(\mathrm{6}{u}^{\mathrm{2}} +\mathrm{2}{v}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{4}\left(\mathrm{3}{u}^{\mathrm{2}} +{v}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{2}\left(\mathrm{9}{u}^{\mathrm{4}} +\mathrm{6}{u}^{\mathrm{2}} {v}^{\mathrm{2}} +{v}^{\mathrm{4}} \right)= \\ $$$$=\mathrm{4}×\mathrm{4}=\mathrm{16}\:\Rightarrow\:\mathrm{6}{u}^{\mathrm{2}} +\mathrm{2}{v}^{\mathrm{2}} =\mathrm{4}\:\Rightarrow\:...\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} =\mathrm{4}\:\Rightarrow \\ $$$$\Rightarrow\:{a}^{\mathrm{6}} +{b}^{\mathrm{6}} +{c}^{\mathrm{6}} =\mathrm{4} \\ $$
