
Question Number 139814 by help last updated on 01/May/21

Answered by physicstutes last updated on 01/May/21
![PV = nRT and P increases at a rate of 0.10 atm/min and V is decreasing at a rate of 0.15 L/min when n = 10 T = ((PV)/(nR)) ⇒ (dT/dt) = (1/(nR))(V_0 (dP/dt)+P_0 (dV/dt)) ⇒ (dT/dt) = (1/((10)(0.0281)))[(10)(0.10) +(8.0)(−0.15)] corrections please if you spot any errors](Q139855.png)
$${PV}\:=\:{nRT} \\ $$$$\mathrm{and}\:{P}\:\mathrm{increases}\:\mathrm{at}\:\mathrm{a}\:\mathrm{rate}\:\mathrm{of}\:\mathrm{0}.\mathrm{10}\:\mathrm{atm}/\mathrm{min}\:\mathrm{and}\:{V}\:\mathrm{is}\:\mathrm{decreasing}\:\mathrm{at} \\ $$$$\:\mathrm{a}\:\mathrm{rate}\:\mathrm{of}\:\mathrm{0}.\mathrm{15}\:\mathrm{L}/\mathrm{min}\:\mathrm{when}\:{n}\:=\:\mathrm{10}\: \\ $$$${T}\:=\:\frac{{PV}}{{nR}}\:\Rightarrow\:\frac{{dT}}{{dt}}\:=\:\frac{\mathrm{1}}{{nR}}\left({V}_{\mathrm{0}} \frac{{dP}}{{dt}}+{P}_{\mathrm{0}} \frac{{dV}}{{dt}}\right) \\ $$$$\Rightarrow\:\frac{{dT}}{{dt}}\:=\:\frac{\mathrm{1}}{\left(\mathrm{10}\right)\left(\mathrm{0}.\mathrm{0281}\right)}\left[\left(\mathrm{10}\right)\left(\mathrm{0}.\mathrm{10}\right)\:+\left(\mathrm{8}.\mathrm{0}\right)\left(−\mathrm{0}.\mathrm{15}\right)\right] \\ $$$$\boldsymbol{{corrections}}\:\boldsymbol{{please}}\:\boldsymbol{{if}}\:\boldsymbol{{you}}\:\boldsymbol{{spot}}\:\boldsymbol{{any}}\:\boldsymbol{{errors}} \\ $$
Answered by Dwaipayan Shikari last updated on 01/May/21
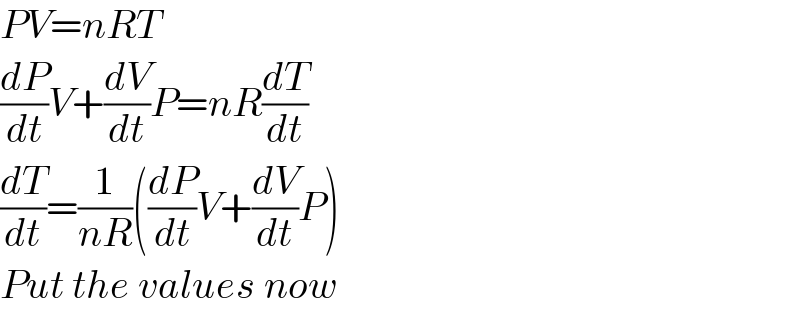
$${PV}={nRT} \\ $$$$\frac{{dP}}{{dt}}{V}+\frac{{dV}}{{dt}}{P}={nR}\frac{{dT}}{{dt}} \\ $$$$\frac{{dT}}{{dt}}=\frac{\mathrm{1}}{{nR}}\left(\frac{{dP}}{{dt}}{V}+\frac{{dV}}{{dt}}{P}\right) \\ $$$${Put}\:{the}\:{values}\:{now} \\ $$
