
Question Number 139778 by chiamaka last updated on 01/May/21
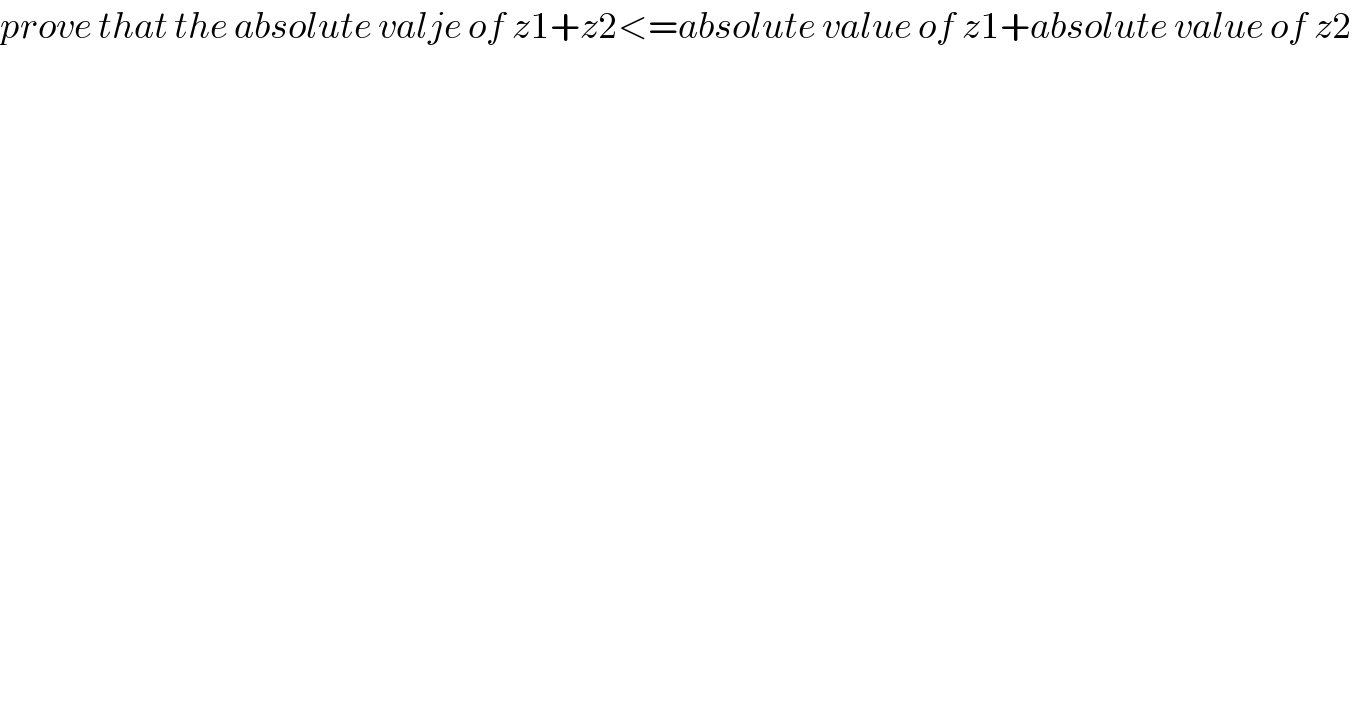
$${prove}\:{that}\:{the}\:{absolute}\:{valje}\:{of}\:{z}\mathrm{1}+{z}\mathrm{2}<={absolute}\:{value}\:{of}\:{z}\mathrm{1}+{absolute}\:{value}\:{of}\:{z}\mathrm{2} \\ $$
Answered by mr W last updated on 01/May/21
Commented bymr W last updated on 01/May/21
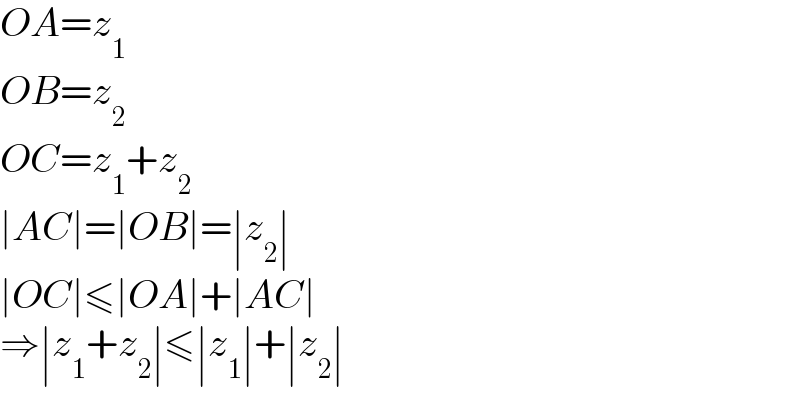
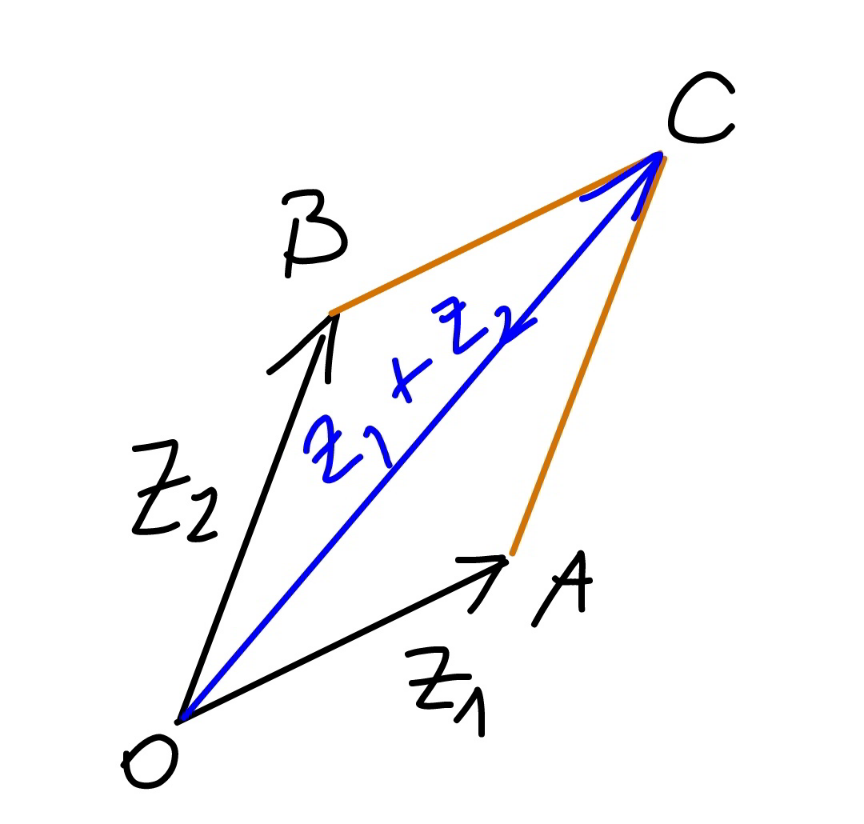
$${OA}={z}_{\mathrm{1}} \\ $$ $${OB}={z}_{\mathrm{2}} \\ $$ $${OC}={z}_{\mathrm{1}} +{z}_{\mathrm{2}} \\ $$ $$\mid{AC}\mid=\mid{OB}\mid=\mid{z}_{\mathrm{2}} \mid \\ $$ $$\mid{OC}\mid\leqslant\mid{OA}\mid+\mid{AC}\mid \\ $$ $$\Rightarrow\mid{z}_{\mathrm{1}} +{z}_{\mathrm{2}} \mid\leqslant\mid{z}_{\mathrm{1}} \mid+\mid{z}_{\mathrm{2}} \mid \\ $$
Answered by mr W last updated on 01/May/21
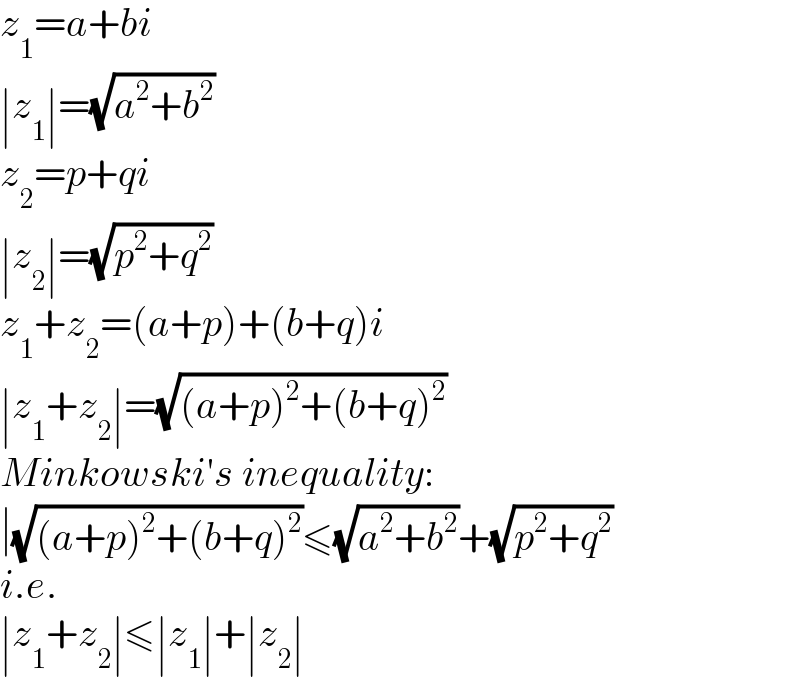
$${z}_{\mathrm{1}} ={a}+{bi} \\ $$ $$\mid{z}_{\mathrm{1}} \mid=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$ $${z}_{\mathrm{2}} ={p}+{qi} \\ $$ $$\mid{z}_{\mathrm{2}} \mid=\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} } \\ $$ $${z}_{\mathrm{1}} +{z}_{\mathrm{2}} =\left({a}+{p}\right)+\left({b}+{q}\right){i} \\ $$ $$\mid{z}_{\mathrm{1}} +{z}_{\mathrm{2}} \mid=\sqrt{\left({a}+{p}\right)^{\mathrm{2}} +\left({b}+{q}\right)^{\mathrm{2}} } \\ $$ $${Minkowski}'{s}\:{inequality}: \\ $$ $$\mid\sqrt{\left({a}+{p}\right)^{\mathrm{2}} +\left({b}+{q}\right)^{\mathrm{2}} }\leqslant\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }+\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} } \\ $$ $${i}.{e}. \\ $$ $$\mid{z}_{\mathrm{1}} +{z}_{\mathrm{2}} \mid\leqslant\mid{z}_{\mathrm{1}} \mid+\mid{z}_{\mathrm{2}} \mid \\ $$
