
Question Number 139756 by cherokeesay last updated on 01/May/21
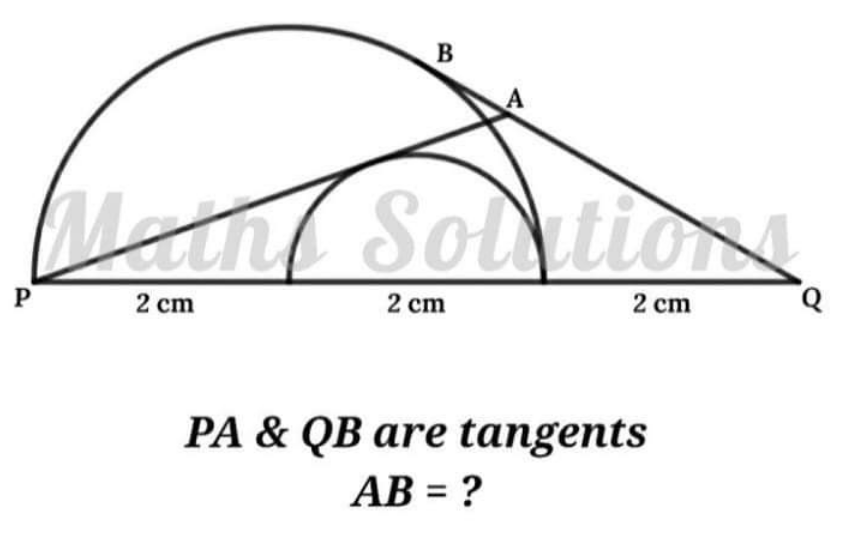
Answered by mr W last updated on 01/May/21
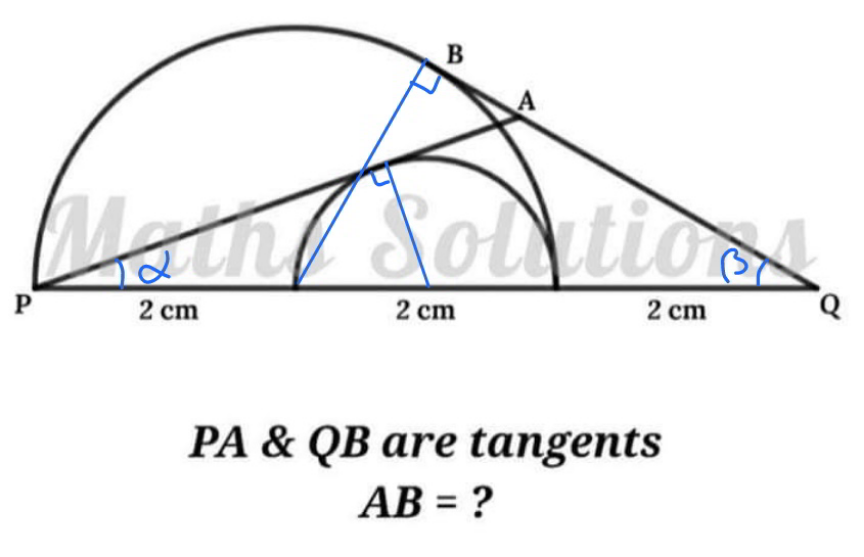
Commented by mr W last updated on 01/May/21
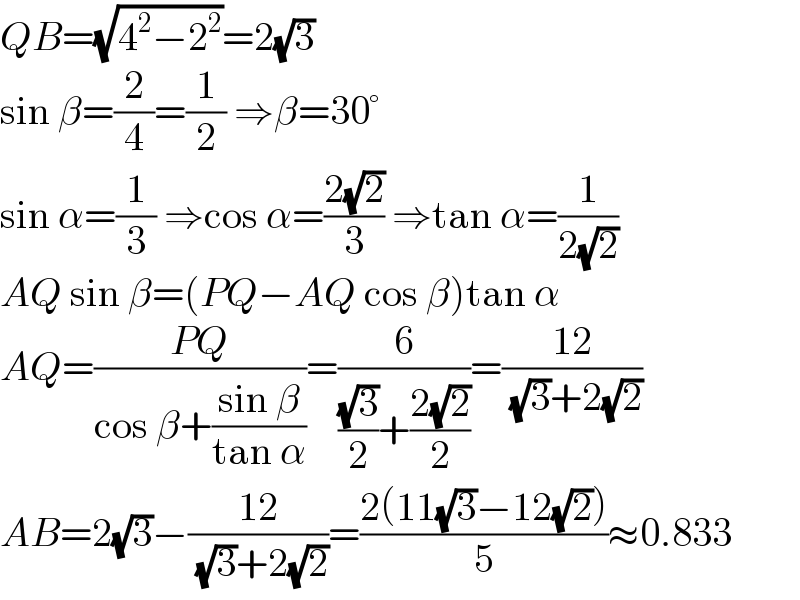
$${QB}=\sqrt{\mathrm{4}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} }=\mathrm{2}\sqrt{\mathrm{3}} \\ $$$$\mathrm{sin}\:\beta=\frac{\mathrm{2}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\beta=\mathrm{30}° \\ $$$$\mathrm{sin}\:\alpha=\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\mathrm{cos}\:\alpha=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\:\Rightarrow\mathrm{tan}\:\alpha=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$${AQ}\:\mathrm{sin}\:\beta=\left({PQ}−{AQ}\:\mathrm{cos}\:\beta\right)\mathrm{tan}\:\alpha \\ $$$${AQ}=\frac{{PQ}}{\mathrm{cos}\:\beta+\frac{\mathrm{sin}\:\beta}{\mathrm{tan}\:\alpha}}=\frac{\mathrm{6}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{2}}}=\frac{\mathrm{12}}{\:\sqrt{\mathrm{3}}+\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$${AB}=\mathrm{2}\sqrt{\mathrm{3}}−\frac{\mathrm{12}}{\:\sqrt{\mathrm{3}}+\mathrm{2}\sqrt{\mathrm{2}}}=\frac{\mathrm{2}\left(\mathrm{11}\sqrt{\mathrm{3}}−\mathrm{12}\sqrt{\mathrm{2}}\right)}{\mathrm{5}}\approx\mathrm{0}.\mathrm{833} \\ $$
Commented by cherokeesay last updated on 01/May/21

$${thank}\:{you}\:{mr}\:{W} \\ $$
