
Question Number 139672 by mathlove last updated on 30/Apr/21

Answered by MJS_new last updated on 30/Apr/21

$$\left({x}^{{a}} \right)^{{b}} ={x}^{{ab}} \\ $$$$\left({x}^{{a}} \right)^{{a}} ={x}^{{a}^{\mathrm{2}} } \\ $$$$\Rightarrow\:{g}\left({x}\right)={x}^{\sqrt{\mathrm{2}}} \\ $$
Commented by mr W last updated on 30/Apr/21
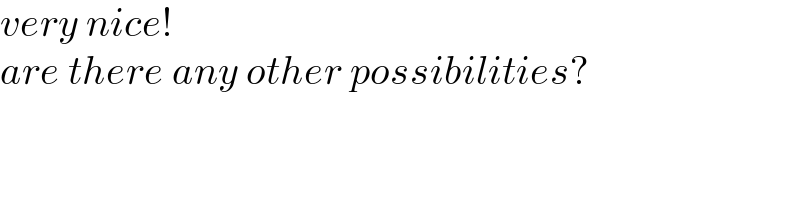
$${very}\:{nice}! \\ $$$${are}\:{there}\:{any}\:{other}\:{possibilities}? \\ $$
Commented by MJS_new last updated on 30/Apr/21
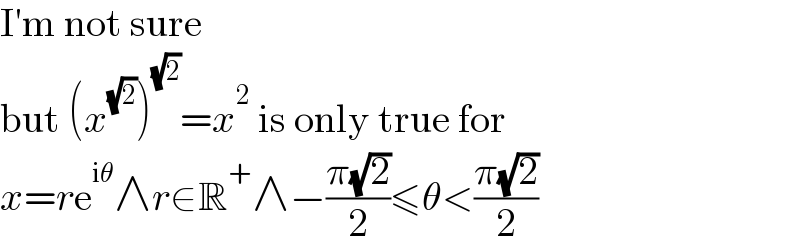
$$\mathrm{I}'\mathrm{m}\:\mathrm{not}\:\mathrm{sure} \\ $$$$\mathrm{but}\:\left({x}^{\sqrt{\mathrm{2}}} \right)^{\sqrt{\mathrm{2}}} ={x}^{\mathrm{2}} \:\mathrm{is}\:\mathrm{only}\:\mathrm{true}\:\mathrm{for} \\ $$$${x}={r}\mathrm{e}^{\mathrm{i}\theta} \wedge{r}\in\mathbb{R}^{+} \wedge−\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{2}}\leqslant\theta<\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$
