
Question Number 17603 by tawa tawa last updated on 08/Jul/17
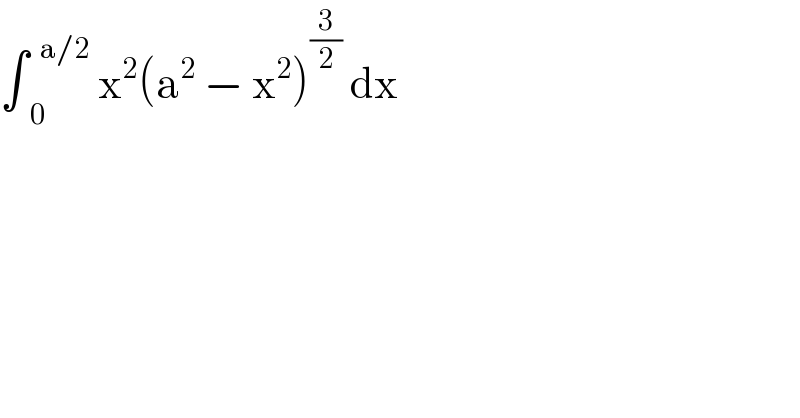
$$\int_{\:\:\mathrm{0}} ^{\:\:\mathrm{a}/\mathrm{2}} \:\mathrm{x}^{\mathrm{2}} \left(\mathrm{a}^{\mathrm{2}} \:−\:\mathrm{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:\mathrm{dx} \\ $$
Answered by alex041103 last updated on 08/Jul/17
![I = ∫_( 0) ^( a/2) x^2 (a^2 − x^2 )^(3/2) dx Let x=asinθ (i.e. θ=sin^(−1) ((x/a))) ⇒dx = acosθ We use 1−sin^2 θ=cos^2 θ and θ=sin^(−1) ((x/a)) to change the limits of integration: I = a^6 ∫_( 0) ^( π/6) sin^2 θcos^4 θ dθ Then we substitute sin^2 θ=1−cos^2 θ I = a^6 [∫_( 0) ^( π/6) cos^4 θ dθ − ∫_( 0) ^( π/6) cos^6 θ dθ] Let I_n =∫_( 0) ^( π/6) cos^n θ dθ ⇒I=a^6 (I_4 −I_6 ) I_n =∫_( 0) ^( π/6) cos^(n−1) θcosθ dθ Then we use integration by parts: u=cos^(n−1) θ dv=cosθ dθ du=(n−1)(−sinθ)cos^(n−2) θ v=sinθ ∫_a ^b u dv = [uv]_a ^b − ∫_a ^b v du I_n = [cos^(n−1) θsinθ]_0 ^(π/6) + (n−1)∫_0 ^(π/6) sin^2 θcos^(n−2) θ dθ We know that sin^2 θ=1−cos^2 θ ⇒I_n = (3^((1/2)(n−1)) /2^n ) + (n−1)(∫_0 ^(π/6) cos^(n−2) θ dθ − ∫_0 ^(π/6) cos^n θ dθ) But I_n =∫_0 ^(π/6) cos^n θ dθ I_(n−2) =∫_0 ^(π/6) cos^(n−2) θ dθ ⇒I_n = (3^((n−1)/2) /2^n ) + (n−1)I_(n−2) − (n−1)I_n i.e. I_n =(3^((n−1)/2) /(n2^n )) + ((n−1)/n)I_(n−2) We use the formula for I=a^6 (I_(6−2) −I_6 ) and we get I=a^6 (I_(6−2) −(((3(√3))/2^7 )+(5/6)I_(6−2) )) =a^6 ((1/6)I_4 −((3(√3))/2^7 )) Now wd use the formula for I_n twice to evaluate I_4 (i.e. expressing I_4 in terms of I_0 ) and we get I_4 =((3(√3))/2^6 )+((3(√3))/2^5 )+(π/2^4 ) Now we finaly get for I: I=∫_0 ^(a/2) x^2 (a^2 −x^2 )^(3/2) dx = ((a^6 π)/(96))](Q17616.png)
$${I}\:=\:\int_{\:\:\mathrm{0}} ^{\:\:\mathrm{a}/\mathrm{2}} \:\mathrm{x}^{\mathrm{2}} \left(\mathrm{a}^{\mathrm{2}} \:−\:\mathrm{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:\mathrm{dx} \\ $$$${Let}\:{x}={asin}\theta\:\left({i}.{e}.\:\theta={sin}^{−\mathrm{1}} \left(\frac{{x}}{{a}}\right)\right) \\ $$$$\Rightarrow{dx}\:=\:{acos}\theta \\ $$$${We}\:{use}\:\mathrm{1}−{sin}^{\mathrm{2}} \theta={cos}^{\mathrm{2}} \theta\:{and}\:\: \\ $$$$\theta={sin}^{−\mathrm{1}} \left(\frac{{x}}{{a}}\right)\:{to}\:{change}\:{the}\:{limits}\:{of} \\ $$$${integration}: \\ $$$${I}\:=\:{a}^{\mathrm{6}} \underset{\:\:\mathrm{0}} {\overset{\:\:\:\:\pi/\mathrm{6}} {\int}}{sin}^{\mathrm{2}} \theta{cos}^{\mathrm{4}} \theta\:{d}\theta \\ $$$${Then}\:{we}\:{substitute}\:{sin}^{\mathrm{2}} \theta=\mathrm{1}−{cos}^{\mathrm{2}} \theta \\ $$$${I}\:=\:{a}^{\mathrm{6}} \left[\underset{\:\mathrm{0}} {\overset{\:\:\:\pi/\mathrm{6}} {\int}}{cos}^{\mathrm{4}} \theta\:{d}\theta\:−\:\underset{\:\:\mathrm{0}} {\overset{\:\:\:\pi/\mathrm{6}} {\int}}{cos}^{\mathrm{6}} \theta\:{d}\theta\right] \\ $$$${Let}\:{I}_{{n}} =\underset{\:\:\mathrm{0}} {\overset{\:\:\:\pi/\mathrm{6}} {\int}}{cos}^{{n}} \theta\:{d}\theta \\ $$$$\Rightarrow{I}={a}^{\mathrm{6}} \left({I}_{\mathrm{4}} −{I}_{\mathrm{6}} \right) \\ $$$${I}_{{n}} =\underset{\:\:\mathrm{0}} {\overset{\:\:\:\pi/\mathrm{6}} {\int}}{cos}^{{n}−\mathrm{1}} \theta{cos}\theta\:{d}\theta \\ $$$${Then}\:{we}\:{use}\:{integration}\:{by}\:{parts}: \\ $$$${u}={cos}^{{n}−\mathrm{1}} \theta\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{dv}={cos}\theta\:{d}\theta \\ $$$${du}=\left({n}−\mathrm{1}\right)\left(−{sin}\theta\right){cos}^{{n}−\mathrm{2}} \theta\:\:\:\:{v}={sin}\theta \\ $$$$\underset{{a}} {\overset{{b}} {\int}}{u}\:{dv}\:=\:\left[{uv}\right]_{{a}} ^{{b}} \:−\:\underset{{a}} {\overset{{b}} {\int}}{v}\:{du} \\ $$$${I}_{{n}} \:=\:\left[{cos}^{{n}−\mathrm{1}} \theta{sin}\theta\right]_{\mathrm{0}} ^{\pi/\mathrm{6}} \:+\:\left({n}−\mathrm{1}\right)\underset{\mathrm{0}} {\overset{\pi/\mathrm{6}} {\int}}{sin}^{\mathrm{2}} \theta{cos}^{{n}−\mathrm{2}} \theta\:{d}\theta \\ $$$${We}\:{know}\:{that}\:{sin}^{\mathrm{2}} \theta=\mathrm{1}−{cos}^{\mathrm{2}} \theta \\ $$$$\Rightarrow{I}_{{n}} \:=\:\frac{\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{2}}\left({n}−\mathrm{1}\right)} }{\mathrm{2}^{{n}} }\:+\:\left({n}−\mathrm{1}\right)\left(\underset{\mathrm{0}} {\overset{\pi/\mathrm{6}} {\int}}{cos}^{{n}−\mathrm{2}} \theta\:{d}\theta\:−\:\underset{\mathrm{0}} {\overset{\pi/\mathrm{6}} {\int}}{cos}^{{n}} \theta\:{d}\theta\right) \\ $$$${But}\: \\ $$$${I}_{{n}} =\underset{\mathrm{0}} {\overset{\pi/\mathrm{6}} {\int}}{cos}^{{n}} \theta\:{d}\theta \\ $$$${I}_{{n}−\mathrm{2}} =\underset{\mathrm{0}} {\overset{\pi/\mathrm{6}} {\int}}{cos}^{{n}−\mathrm{2}} \theta\:{d}\theta \\ $$$$\Rightarrow{I}_{{n}} \:=\:\frac{\mathrm{3}^{\frac{{n}−\mathrm{1}}{\mathrm{2}}} }{\mathrm{2}^{{n}} }\:+\:\left({n}−\mathrm{1}\right){I}_{{n}−\mathrm{2}} \:−\:\left({n}−\mathrm{1}\right){I}_{{n}} \\ $$$${i}.{e}.\:{I}_{{n}} =\frac{\mathrm{3}^{\frac{{n}−\mathrm{1}}{\mathrm{2}}} }{{n}\mathrm{2}^{{n}} }\:+\:\frac{{n}−\mathrm{1}}{{n}}{I}_{{n}−\mathrm{2}} \\ $$$${We}\:{use}\:{the}\:{formula}\:{for}\:{I}={a}^{\mathrm{6}} \left({I}_{\mathrm{6}−\mathrm{2}} −{I}_{\mathrm{6}} \right) \\ $$$${and}\:{we}\:{get} \\ $$$${I}={a}^{\mathrm{6}} \left({I}_{\mathrm{6}−\mathrm{2}} −\left(\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}^{\mathrm{7}} }+\frac{\mathrm{5}}{\mathrm{6}}{I}_{\mathrm{6}−\mathrm{2}} \right)\right) \\ $$$$={a}^{\mathrm{6}} \left(\frac{\mathrm{1}}{\mathrm{6}}{I}_{\mathrm{4}} −\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}^{\mathrm{7}} }\right) \\ $$$${Now}\:{wd}\:{use}\:{the}\:{formula}\:{for}\:{I}_{{n}} \:{twice} \\ $$$${to}\:{evaluate}\:{I}_{\mathrm{4}} \left({i}.{e}.\:{expressing}\:{I}_{\mathrm{4}} \:{in}\:{terms}\:{of}\:{I}_{\mathrm{0}} \right)\:{and}\:{we}\:{get} \\ $$$${I}_{\mathrm{4}} =\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}^{\mathrm{6}} }+\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}^{\mathrm{5}} }+\frac{\pi}{\mathrm{2}^{\mathrm{4}} } \\ $$$${Now}\:{we}\:{finaly}\:{get}\:{for}\:{I}: \\ $$$${I}=\underset{\mathrm{0}} {\overset{{a}/\mathrm{2}} {\int}}{x}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{x}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} \:{dx}\:=\:\frac{{a}^{\mathrm{6}} \pi}{\mathrm{96}} \\ $$$$ \\ $$
Commented by tawa tawa last updated on 08/Jul/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}. \\ $$
Answered by Arnab Maiti last updated on 13/Jul/17
![let I =∫_0 ^( (a/2)) x^2 (a^2 −x^2 )^(3/2) dx put x=a sinθ ∴ dx= a cosθ dθ ∴ I=∫_0 ^( (π/6)) a^3 sin^2 θ{a^2 (1−sin^2 θ)}^(3/2) cosθ dθ =a^6 ∫_0 ^(π/6) sin^2 θ cos^4 θ dθ =a^6 (1/8)∫_0 ^( (π/6)) (2sinθ cosθ)^2 2cos^2 θ dθ =a^6 ×(1/8)∫_0 ^(π/6) sin^2 2θ (1+cos2θ)dθ =a^6 ×(1/8)[∫_0 ^(π/6) sin^2 2θ dθ+∫_0 ^(π/6) sin^2 2θ cos2θ dθ] =a^6 /8×[(1/2)∫_0 ^(π/6) (1−cos4θ)dθ+(1/2)∫_0 ^((√3)/2) (sin 2θ)^2 d(sin 2θ)] =(a^6 /(16))[ θ−((sin 4θ)/4)]_0 ^(π/6) +(a^6 /(16))[(((p)^3 )/3)]_0 ^((√3)/2) let sin2θ=p =(a^6 /(16))[{(π/6)−((√3)/8)}+((3(√3))/(3×8))] =(a^6 /(16))×(π/6)=((πa^6 )/(96))](Q17881.png)
$$\mathrm{let}\:\:\mathrm{I}\:=\int_{\mathrm{0}} ^{\:\frac{\mathrm{a}}{\mathrm{2}}} \mathrm{x}^{\mathrm{2}} \left(\mathrm{a}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} \mathrm{dx} \\ $$$$\mathrm{put}\:\mathrm{x}=\mathrm{a}\:\mathrm{sin}\theta\:\:\therefore\:\mathrm{dx}=\:\mathrm{a}\:\mathrm{cos}\theta\:\mathrm{d}\theta \\ $$$$\therefore\:\mathrm{I}=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{6}}} \mathrm{a}^{\mathrm{3}} \mathrm{sin}^{\mathrm{2}} \theta\left\{\mathrm{a}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta\right)\right\}^{\frac{\mathrm{3}}{\mathrm{2}}} \mathrm{cos}\theta\:\mathrm{d}\theta \\ $$$$=\mathrm{a}^{\mathrm{6}} \int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \mathrm{sin}^{\mathrm{2}} \theta\:\mathrm{cos}^{\mathrm{4}} \theta\:\mathrm{d}\theta \\ $$$$=\mathrm{a}^{\mathrm{6}} \frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{6}}} \left(\mathrm{2sin}\theta\:\mathrm{cos}\theta\right)^{\mathrm{2}} \mathrm{2cos}^{\mathrm{2}} \theta\:\mathrm{d}\theta \\ $$$$=\mathrm{a}^{\mathrm{6}} ×\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \mathrm{sin}^{\mathrm{2}} \mathrm{2}\theta\:\left(\mathrm{1}+\mathrm{cos2}\theta\right)\mathrm{d}\theta \\ $$$$=\mathrm{a}^{\mathrm{6}} ×\frac{\mathrm{1}}{\mathrm{8}}\left[\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \mathrm{sin}^{\mathrm{2}} \mathrm{2}\theta\:\mathrm{d}\theta+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \mathrm{sin}^{\mathrm{2}} \mathrm{2}\theta\:\mathrm{cos2}\theta\:\mathrm{d}\theta\right] \\ $$$$=\mathrm{a}^{\mathrm{6}} /\mathrm{8}×\left[\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \left(\mathrm{1}−\mathrm{cos4}\theta\right)\mathrm{d}\theta+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \left(\mathrm{sin}\:\mathrm{2}\theta\right)^{\mathrm{2}} \mathrm{d}\left(\mathrm{sin}\:\mathrm{2}\theta\right)\right] \\ $$$$=\frac{\mathrm{a}^{\mathrm{6}} }{\mathrm{16}}\left[\:\theta−\frac{\mathrm{sin}\:\mathrm{4}\theta}{\mathrm{4}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} +\frac{\mathrm{a}^{\mathrm{6}} }{\mathrm{16}}\left[\frac{\left(\mathrm{p}\right)^{\mathrm{3}} }{\mathrm{3}}\right]_{\mathrm{0}} ^{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \:\:\:\mathrm{let}\:\mathrm{sin2}\theta=\mathrm{p} \\ $$$$=\frac{\mathrm{a}^{\mathrm{6}} }{\mathrm{16}}\left[\left\{\frac{\pi}{\mathrm{6}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{8}}\right\}+\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{3}×\mathrm{8}}\right] \\ $$$$=\frac{\mathrm{a}^{\mathrm{6}} }{\mathrm{16}}×\frac{\pi}{\mathrm{6}}=\frac{\pi\mathrm{a}^{\mathrm{6}} }{\mathrm{96}} \\ $$
Commented by tawa tawa last updated on 11/Jul/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by alex041103 last updated on 11/Jul/17
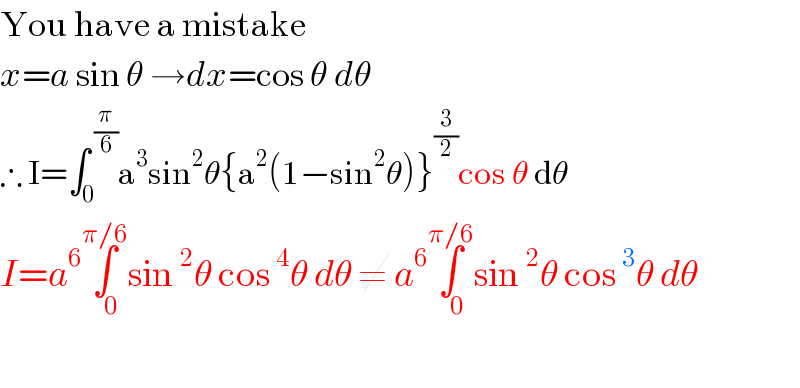
$$\mathrm{You}\:\mathrm{have}\:\mathrm{a}\:\mathrm{mistake} \\ $$$${x}={a}\:\mathrm{sin}\:\theta\:\rightarrow{dx}=\mathrm{cos}\:\theta\:{d}\theta \\ $$$$\therefore\:\mathrm{I}=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{6}}} \mathrm{a}^{\mathrm{3}} \mathrm{sin}^{\mathrm{2}} \theta\left\{\mathrm{a}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta\right)\right\}^{\frac{\mathrm{3}}{\mathrm{2}}} \mathrm{cos}\:\theta\:\mathrm{d}\theta \\ $$$${I}={a}^{\mathrm{6}} \underset{\:\:\:\mathrm{0}} {\overset{\pi/\mathrm{6}} {\int}}\mathrm{sin}\:^{\mathrm{2}} \theta\:\mathrm{cos}\:^{\mathrm{4}} \theta\:{d}\theta\:\neq\:{a}^{\mathrm{6}} \underset{\:\:\:\mathrm{0}} {\overset{\pi/\mathrm{6}} {\int}}\mathrm{sin}\:^{\mathrm{2}} \theta\:\mathrm{cos}\:^{\mathrm{3}} \theta\:{d}\theta \\ $$$$ \\ $$
Commented by Arnab Maiti last updated on 12/Jul/17
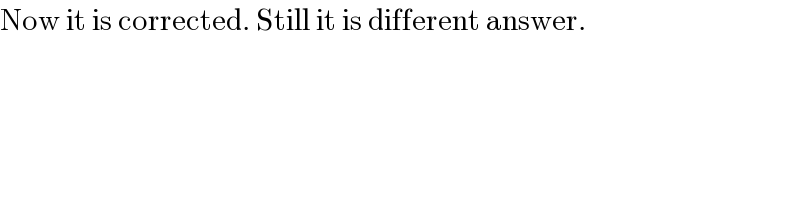
$$\mathrm{Now}\:\mathrm{it}\:\mathrm{is}\:\mathrm{corrected}.\:\mathrm{Still}\:\mathrm{it}\:\mathrm{is}\:\mathrm{different}\:\mathrm{answer}. \\ $$
Commented by alex041103 last updated on 13/Jul/17
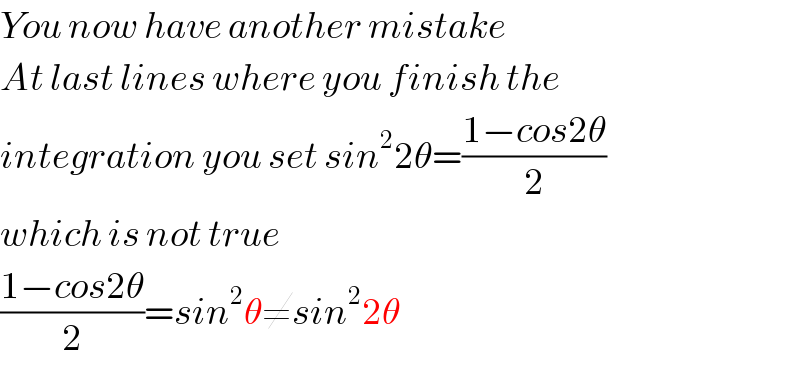
$${You}\:{now}\:{have}\:{another}\:{mistake} \\ $$$${At}\:{last}\:{lines}\:{where}\:{you}\:{finish}\:{the} \\ $$$${integration}\:{you}\:{set}\:{sin}^{\mathrm{2}} \mathrm{2}\theta=\frac{\mathrm{1}−{cos}\mathrm{2}\theta}{\mathrm{2}} \\ $$$${which}\:{is}\:{not}\:{true} \\ $$$$\frac{\mathrm{1}−{cos}\mathrm{2}\theta}{\mathrm{2}}={sin}^{\mathrm{2}} \theta\neq{sin}^{\mathrm{2}} \mathrm{2}\theta \\ $$
Commented by Arnab Maiti last updated on 13/Jul/17

$$\mathrm{The}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{indentical}\:\mathrm{now}. \\ $$$$\mathrm{Thank}\:\mathrm{you}!! \\ $$
