
Question Number 139587 by mathlove last updated on 29/Apr/21
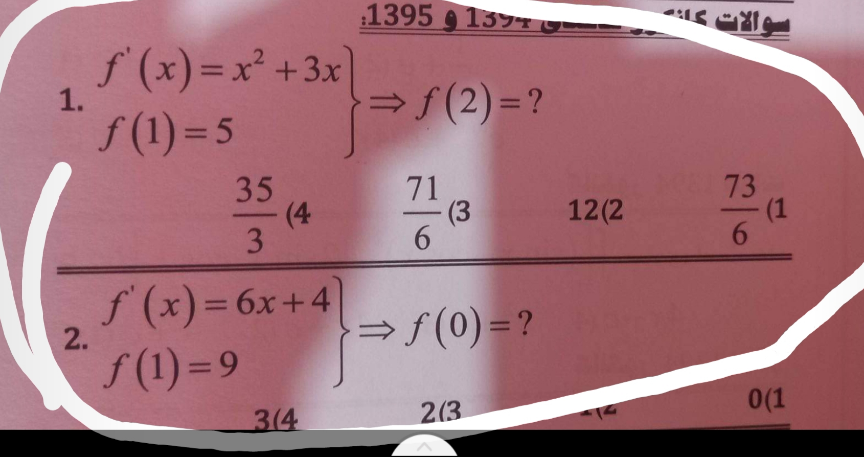
Answered by qaz last updated on 29/Apr/21
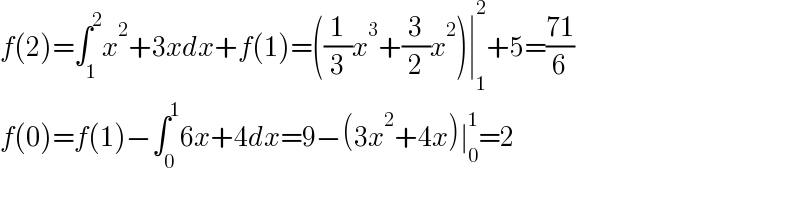
$${f}\left(\mathrm{2}\right)=\int_{\mathrm{1}} ^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{3}{xdx}+{f}\left(\mathrm{1}\right)=\left(\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} +\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}} \right)\mid_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{5}=\frac{\mathrm{71}}{\mathrm{6}} \\ $$$${f}\left(\mathrm{0}\right)={f}\left(\mathrm{1}\right)−\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{6}{x}+\mathrm{4}{dx}=\mathrm{9}−\left(\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}{x}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{2} \\ $$
