
Question Number 139456 by SOMEDAVONG last updated on 27/Apr/21
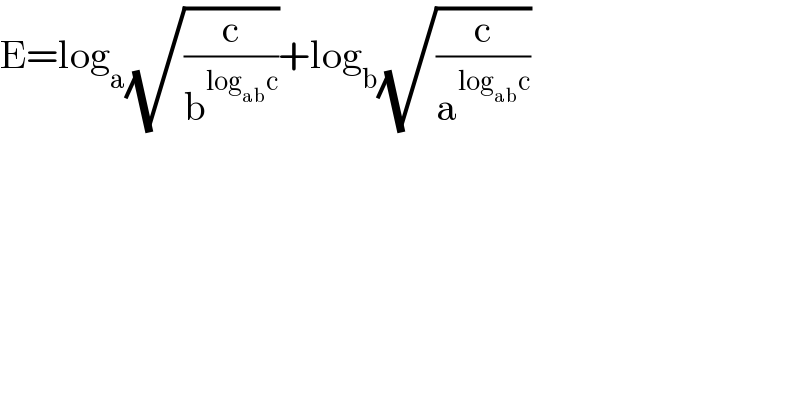
$$\mathrm{E}=\mathrm{log}_{\mathrm{a}} \sqrt{\frac{\mathrm{c}}{\mathrm{b}^{\mathrm{log}_{\mathrm{ab}} \mathrm{c}} }}+\mathrm{log}_{\mathrm{b}} \sqrt{\frac{\mathrm{c}}{\mathrm{a}^{\mathrm{log}_{\mathrm{ab}} \mathrm{c}} }} \\ $$
Answered by bemath last updated on 27/Apr/21
![E = log _a (√(c/c^(log _(ab) b) )) + log _b (√(c/c^(log _(ab) a) )) E=(1/2)[ log _a (c^(1−log _(ab) b) )+log _b (c^(1−log _(ab) a) )] E=(1/2) [ log _a (c^(log _(ab) ((1/a))) )+ log _b (c^(log _(ab) ((1/b))) )]](Q139472.png)
$$\mathrm{E}\:=\:\mathrm{log}\:_{\mathrm{a}} \sqrt{\frac{\mathrm{c}}{\mathrm{c}^{\mathrm{log}\:_{\mathrm{ab}} \mathrm{b}} }}\:+\:\mathrm{log}\:_{\mathrm{b}} \sqrt{\frac{\mathrm{c}}{\mathrm{c}^{\mathrm{log}\:_{\mathrm{ab}} \mathrm{a}} }} \\ $$$$\mathrm{E}=\frac{\mathrm{1}}{\mathrm{2}}\left[\:\mathrm{log}\:_{\mathrm{a}} \left(\mathrm{c}^{\mathrm{1}−\mathrm{log}\:_{\mathrm{ab}} \mathrm{b}} \right)+\mathrm{log}\:_{\mathrm{b}} \left(\mathrm{c}^{\mathrm{1}−\mathrm{log}\:_{\mathrm{ab}} \mathrm{a}} \right)\right] \\ $$$$\mathrm{E}=\frac{\mathrm{1}}{\mathrm{2}}\:\left[\:\mathrm{log}\:_{\mathrm{a}} \left(\mathrm{c}^{\mathrm{log}\:_{\mathrm{ab}} \left(\frac{\mathrm{1}}{\mathrm{a}}\right)} \right)+\:\mathrm{log}\:_{\mathrm{b}} \left(\mathrm{c}^{\mathrm{log}\:_{\mathrm{ab}} \left(\frac{\mathrm{1}}{\mathrm{b}}\right)} \right)\right] \\ $$$$ \\ $$
