
Question Number 139445 by aliibrahim1 last updated on 27/Apr/21

Answered by mr W last updated on 27/Apr/21
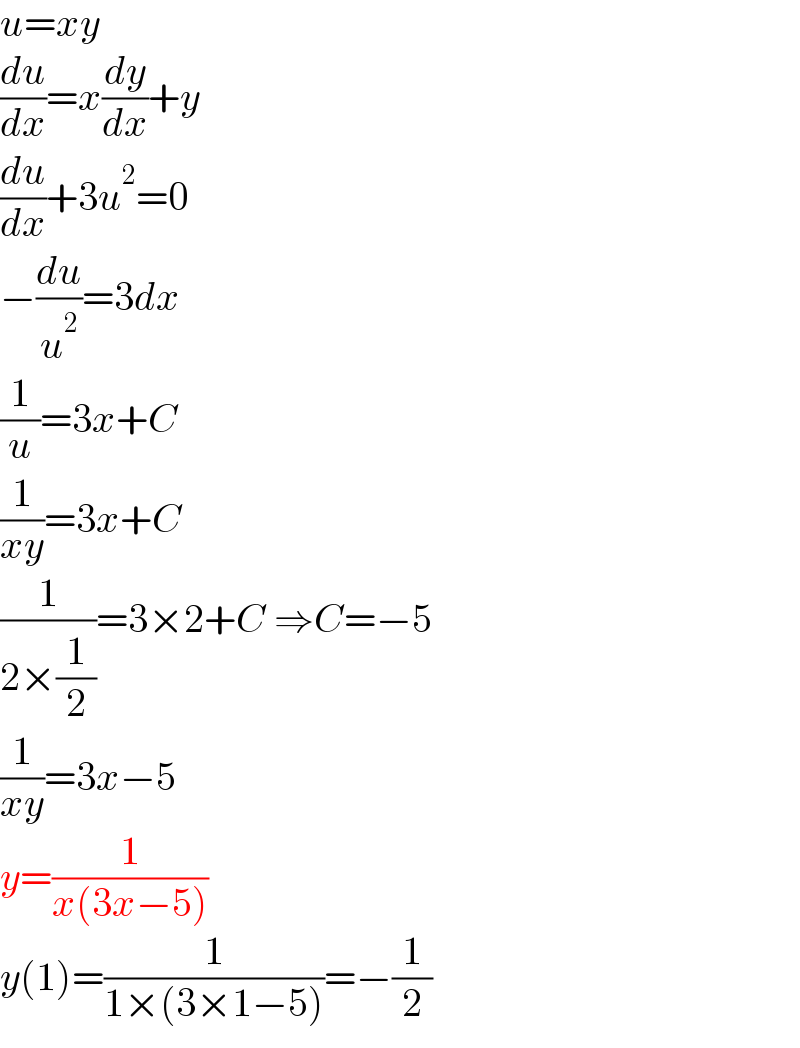
$${u}={xy} \\ $$$$\frac{{du}}{{dx}}={x}\frac{{dy}}{{dx}}+{y} \\ $$$$\frac{{du}}{{dx}}+\mathrm{3}{u}^{\mathrm{2}} =\mathrm{0} \\ $$$$−\frac{{du}}{{u}^{\mathrm{2}} }=\mathrm{3}{dx} \\ $$$$\frac{\mathrm{1}}{{u}}=\mathrm{3}{x}+{C} \\ $$$$\frac{\mathrm{1}}{{xy}}=\mathrm{3}{x}+{C} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}}=\mathrm{3}×\mathrm{2}+{C}\:\Rightarrow{C}=−\mathrm{5} \\ $$$$\frac{\mathrm{1}}{{xy}}=\mathrm{3}{x}−\mathrm{5} \\ $$$${y}=\frac{\mathrm{1}}{{x}\left(\mathrm{3}{x}−\mathrm{5}\right)} \\ $$$${y}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{1}×\left(\mathrm{3}×\mathrm{1}−\mathrm{5}\right)}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by aliibrahim1 last updated on 27/Apr/21

$${thx}\:{bro} \\ $$
