
Question Number 139331 by 7770 last updated on 26/Apr/21
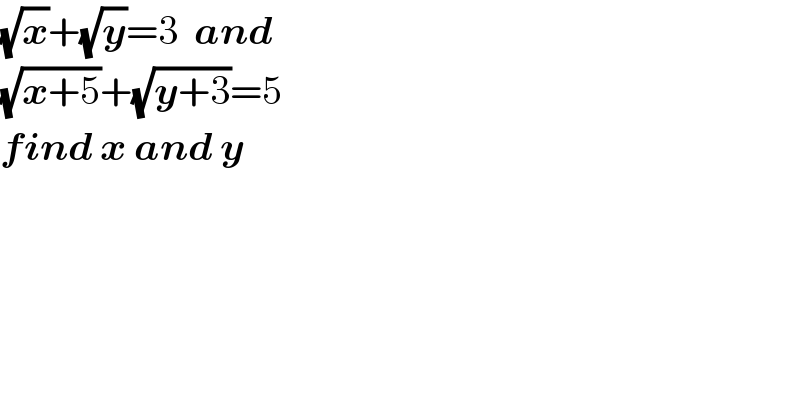
$$\sqrt{\boldsymbol{{x}}}+\sqrt{\boldsymbol{{y}}}=\mathrm{3}\:\:\boldsymbol{{and}} \\ $$$$\sqrt{\boldsymbol{{x}}+\mathrm{5}}+\sqrt{\boldsymbol{{y}}+\mathrm{3}}=\mathrm{5} \\ $$$$\boldsymbol{{find}}\:\boldsymbol{{x}}\:\boldsymbol{{and}}\:\boldsymbol{{y}} \\ $$
Answered by bemath last updated on 26/Apr/21
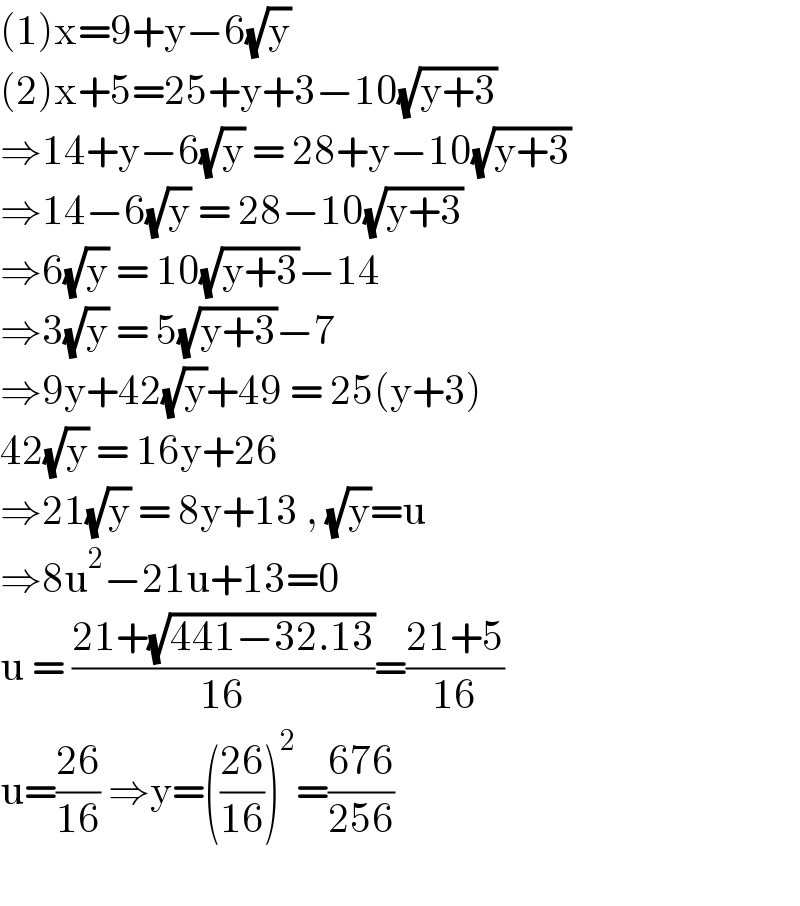
$$\left(\mathrm{1}\right)\mathrm{x}=\mathrm{9}+\mathrm{y}−\mathrm{6}\sqrt{\mathrm{y}}\: \\ $$$$\left(\mathrm{2}\right)\mathrm{x}+\mathrm{5}=\mathrm{25}+\mathrm{y}+\mathrm{3}−\mathrm{10}\sqrt{\mathrm{y}+\mathrm{3}} \\ $$$$\Rightarrow\mathrm{14}+\mathrm{y}−\mathrm{6}\sqrt{\mathrm{y}}\:=\:\mathrm{28}+\mathrm{y}−\mathrm{10}\sqrt{\mathrm{y}+\mathrm{3}} \\ $$$$\Rightarrow\mathrm{14}−\mathrm{6}\sqrt{\mathrm{y}}\:=\:\mathrm{28}−\mathrm{10}\sqrt{\mathrm{y}+\mathrm{3}} \\ $$$$\Rightarrow\mathrm{6}\sqrt{\mathrm{y}}\:=\:\mathrm{10}\sqrt{\mathrm{y}+\mathrm{3}}−\mathrm{14} \\ $$$$\Rightarrow\mathrm{3}\sqrt{\mathrm{y}}\:=\:\mathrm{5}\sqrt{\mathrm{y}+\mathrm{3}}−\mathrm{7} \\ $$$$\Rightarrow\mathrm{9y}+\mathrm{42}\sqrt{\mathrm{y}}+\mathrm{49}\:=\:\mathrm{25}\left(\mathrm{y}+\mathrm{3}\right) \\ $$$$\mathrm{42}\sqrt{\mathrm{y}}\:=\:\mathrm{16y}+\mathrm{26} \\ $$$$\Rightarrow\mathrm{21}\sqrt{\mathrm{y}}\:=\:\mathrm{8y}+\mathrm{13}\:,\:\sqrt{\mathrm{y}}=\mathrm{u} \\ $$$$\Rightarrow\mathrm{8u}^{\mathrm{2}} −\mathrm{21u}+\mathrm{13}=\mathrm{0} \\ $$$$\mathrm{u}\:=\:\frac{\mathrm{21}+\sqrt{\mathrm{441}−\mathrm{32}.\mathrm{13}}}{\mathrm{16}}=\frac{\mathrm{21}+\mathrm{5}}{\mathrm{16}} \\ $$$$\mathrm{u}=\frac{\mathrm{26}}{\mathrm{16}}\:\Rightarrow\mathrm{y}=\left(\frac{\mathrm{26}}{\mathrm{16}}\right)^{\mathrm{2}} =\frac{\mathrm{676}}{\mathrm{256}} \\ $$$$ \\ $$
Answered by MJS_new last updated on 26/Apr/21

$${x}\geqslant\mathrm{0}\wedge{y}\geqslant\mathrm{0} \\ $$$$\left(\mathrm{1}\right)\:{y}=\left(\mathrm{3}−\sqrt{{x}}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\:{y}=\left(\mathrm{5}−\sqrt{{x}+\mathrm{5}}\right)^{\mathrm{2}} −\mathrm{3} \\ $$$$\Rightarrow \\ $$$$\left(\mathrm{3}−\sqrt{{x}}\right)^{\mathrm{2}} −\left(\mathrm{5}−\sqrt{{x}+\mathrm{5}}\right)^{\mathrm{2}} +\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{5}\sqrt{{x}+\mathrm{5}}−\mathrm{3}\sqrt{{x}}=\mathrm{9} \\ $$$$\mathrm{squaring}\:\mathrm{and}\:\mathrm{transforming} \\ $$$$\mathrm{17}{x}+\mathrm{22}=\mathrm{15}\sqrt{{x}}\sqrt{{x}+\mathrm{5}} \\ $$$$\mathrm{squaring}\:\mathrm{and}\:\mathrm{transforming} \\ $$$${x}^{\mathrm{2}} −\frac{\mathrm{377}}{\mathrm{64}}{x}+\frac{\mathrm{121}}{\mathrm{16}}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =\mathrm{4}\wedge{x}_{\mathrm{2}} =\frac{\mathrm{121}}{\mathrm{64}}\:\Rightarrow\:{y}_{\mathrm{1}} =\mathrm{1}\wedge{y}_{\mathrm{2}} =\frac{\mathrm{169}}{\mathrm{64}} \\ $$
