
Question Number 139319 by mathsuji last updated on 25/Apr/21
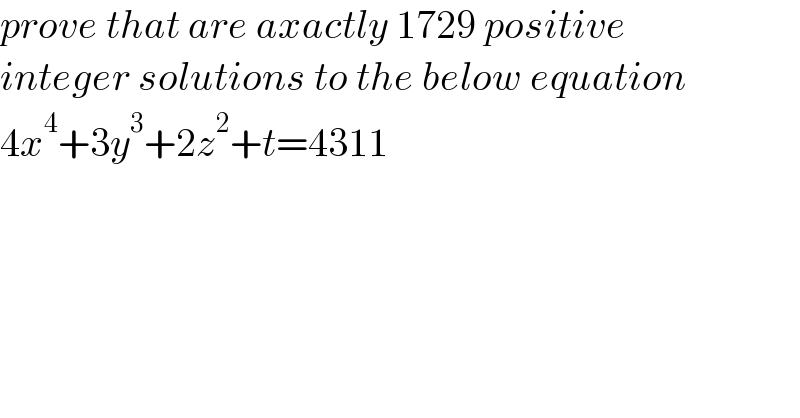
$${prove}\:{that}\:{are}\:{axactly}\:\mathrm{1729}\:{positive} \\ $$$${integer}\:{solutions}\:{to}\:{the}\:{below}\:{equation} \\ $$$$\mathrm{4}{x}^{\mathrm{4}} +\mathrm{3}{y}^{\mathrm{3}} +\mathrm{2}{z}^{\mathrm{2}} +{t}=\mathrm{4311} \\ $$
Commented by Rasheed.Sindhi last updated on 27/Apr/21
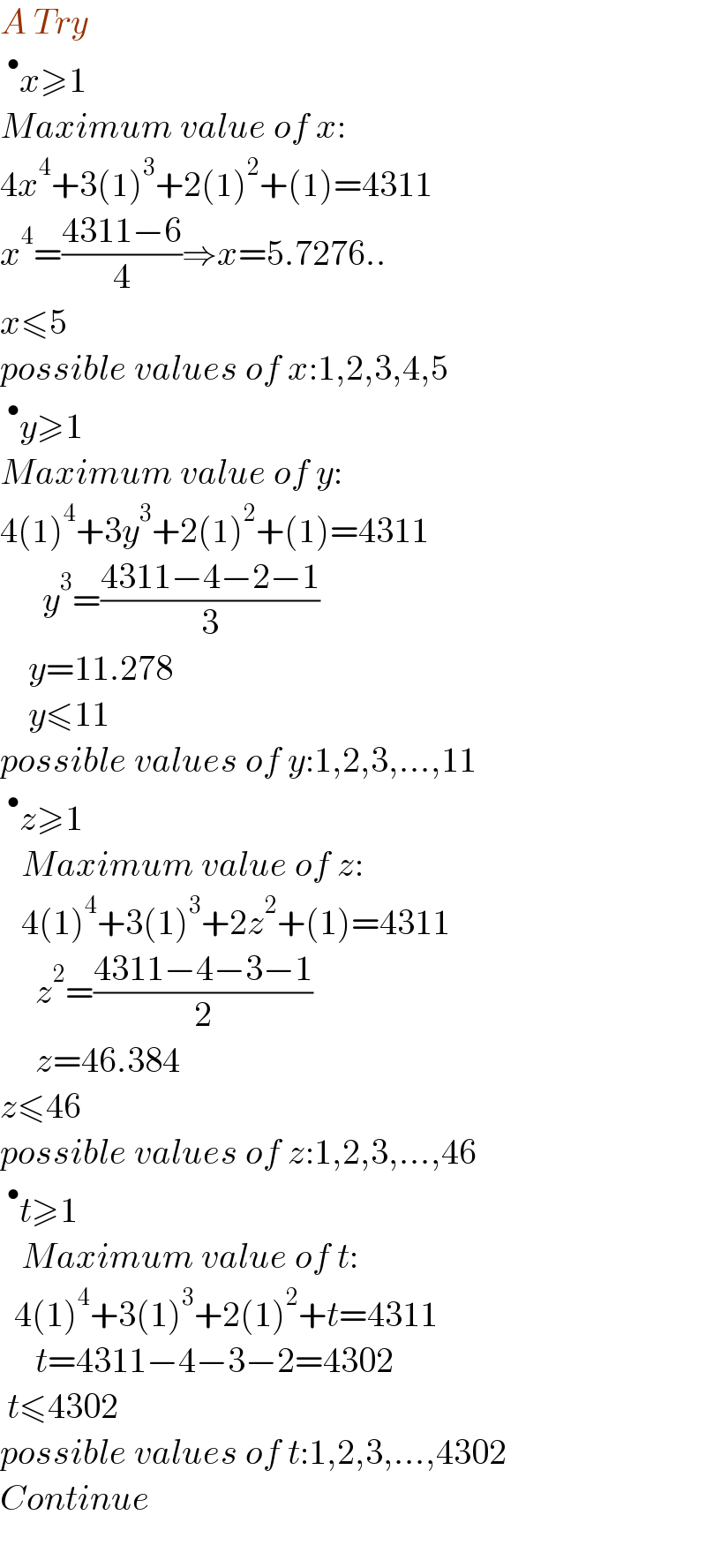
$${A}\:{Try} \\ $$$$\:^{\bullet} {x}\geqslant\mathrm{1} \\ $$$${Maximum}\:{value}\:{of}\:{x}: \\ $$$$\mathrm{4}{x}^{\mathrm{4}} +\mathrm{3}\left(\mathrm{1}\right)^{\mathrm{3}} +\mathrm{2}\left(\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{1}\right)=\mathrm{4311} \\ $$$${x}^{\mathrm{4}} =\frac{\mathrm{4311}−\mathrm{6}}{\mathrm{4}}\Rightarrow{x}=\mathrm{5}.\mathrm{7276}.. \\ $$$${x}\leqslant\mathrm{5} \\ $$$${possible}\:{values}\:{of}\:{x}:\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5} \\ $$$$\:^{\bullet} {y}\geqslant\mathrm{1} \\ $$$${Maximum}\:{value}\:{of}\:{y}: \\ $$$$\mathrm{4}\left(\mathrm{1}\right)^{\mathrm{4}} +\mathrm{3}{y}^{\mathrm{3}} +\mathrm{2}\left(\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{1}\right)=\mathrm{4311} \\ $$$$\:\:\:\:\:\:{y}^{\mathrm{3}} =\frac{\mathrm{4311}−\mathrm{4}−\mathrm{2}−\mathrm{1}}{\mathrm{3}} \\ $$$$\:\:\:\:{y}=\mathrm{11}.\mathrm{278} \\ $$$$\:\:\:\:{y}\leqslant\mathrm{11} \\ $$$${possible}\:{values}\:{of}\:{y}:\mathrm{1},\mathrm{2},\mathrm{3},...,\mathrm{11} \\ $$$$\:^{\bullet} {z}\geqslant\mathrm{1} \\ $$$$\:\:\:{Maximum}\:{value}\:{of}\:{z}: \\ $$$$\:\:\:\mathrm{4}\left(\mathrm{1}\right)^{\mathrm{4}} +\mathrm{3}\left(\mathrm{1}\right)^{\mathrm{3}} +\mathrm{2}{z}^{\mathrm{2}} +\left(\mathrm{1}\right)=\mathrm{4311} \\ $$$$\:\:\:\:\:{z}^{\mathrm{2}} =\frac{\mathrm{4311}−\mathrm{4}−\mathrm{3}−\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:\:{z}=\mathrm{46}.\mathrm{384} \\ $$$${z}\leqslant\mathrm{46} \\ $$$${possible}\:{values}\:{of}\:{z}:\mathrm{1},\mathrm{2},\mathrm{3},...,\mathrm{46} \\ $$$$\:^{\bullet} {t}\geqslant\mathrm{1} \\ $$$$\:\:\:{Maximum}\:{value}\:{of}\:{t}: \\ $$$$\:\:\mathrm{4}\left(\mathrm{1}\right)^{\mathrm{4}} +\mathrm{3}\left(\mathrm{1}\right)^{\mathrm{3}} +\mathrm{2}\left(\mathrm{1}\right)^{\mathrm{2}} +{t}=\mathrm{4311} \\ $$$$\:\:\:\:\:{t}=\mathrm{4311}−\mathrm{4}−\mathrm{3}−\mathrm{2}=\mathrm{4302} \\ $$$$\:{t}\leqslant\mathrm{4302} \\ $$$${possible}\:{values}\:{of}\:{t}:\mathrm{1},\mathrm{2},\mathrm{3},...,\mathrm{4302} \\ $$$${Continue} \\ $$$$ \\ $$
Commented by mathsuji last updated on 28/Apr/21
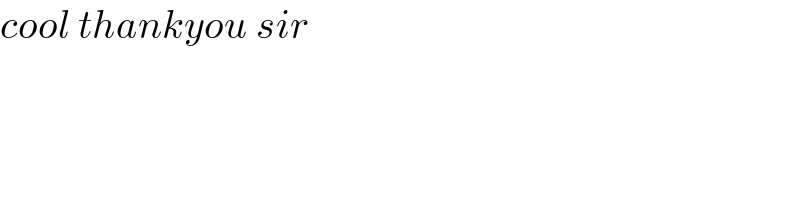
$${cool}\:{thankyou}\:{sir} \\ $$
