
Question Number 13929 by ajfour last updated on 25/May/17
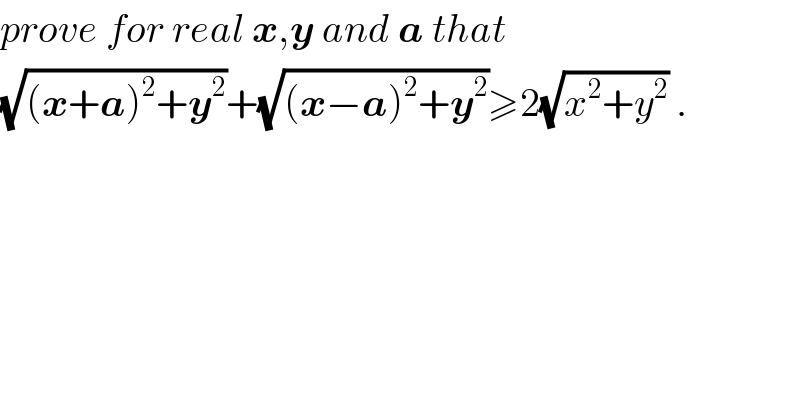
$${prove}\:{for}\:{real}\:\boldsymbol{{x}},\boldsymbol{{y}}\:{and}\:\boldsymbol{{a}}\:{that} \\ $$$$\sqrt{\left(\boldsymbol{{x}}+\boldsymbol{{a}}\right)^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} }+\sqrt{\left(\boldsymbol{{x}}−\boldsymbol{{a}}\right)^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} }\geqslant\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:. \\ $$$$ \\ $$
Answered by mrW1 last updated on 25/May/17

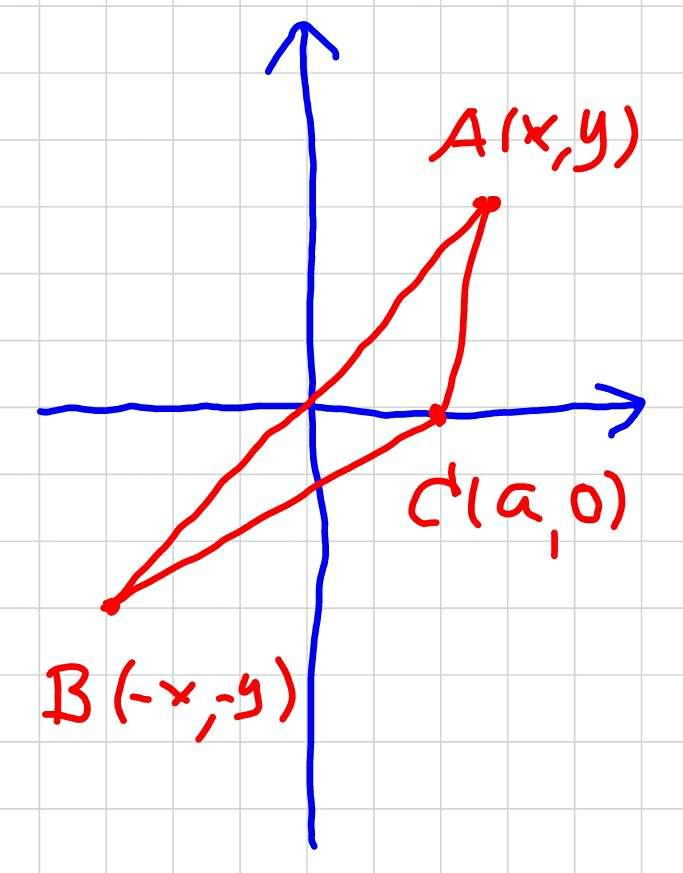
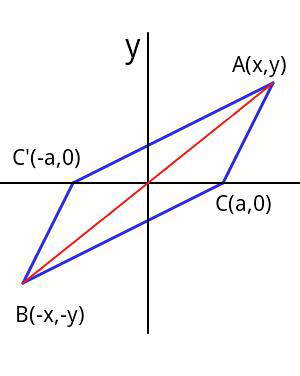
$${Let}'{s}\:{consider}\:\mathrm{3}\:{points}\:{in}\:{coordinate} \\ $$$${system}: \\ $$$${A}\left({x},{y}\right) \\ $$$${B}\left(−{x},−{y}\right) \\ $$$${C}\left({a},\mathrm{0}\right) \\ $$$${BC}=\sqrt{\left({x}+{a}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$${CA}=\sqrt{\left({x}−{a}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$${BA}=\sqrt{\left(\mathrm{2}{x}\right)^{\mathrm{2}} +\left(\mathrm{2}{y}\right)^{\mathrm{2}} }=\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$$ \\ $$$${In}\:{the}\:{triangle}\:\Delta{ABC}\:{we}\:{have} \\ $$$${BC}+{CA}\geqslant{BA} \\ $$$$\Rightarrow\sqrt{\left({x}+{a}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} }+\sqrt{\left({x}−{a}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} }\geqslant\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$
Commented by mrW1 last updated on 25/May/17
Commented by ajfour last updated on 25/May/17
Commented by ajfour last updated on 25/May/17
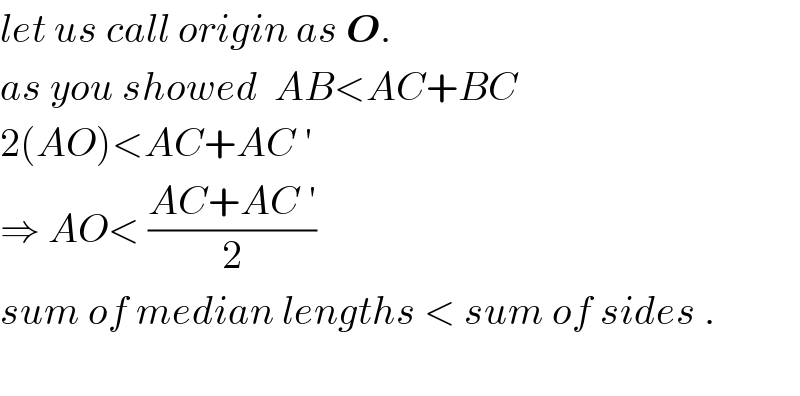
$${let}\:{us}\:{call}\:{origin}\:{as}\:\boldsymbol{{O}}. \\ $$$${as}\:{you}\:{showed}\:\:{AB}<{AC}+{BC} \\ $$$$\mathrm{2}\left({AO}\right)<{AC}+{AC}\:' \\ $$$$\Rightarrow\:{AO}<\:\frac{{AC}+{AC}\:'}{\mathrm{2}}\: \\ $$$${sum}\:{of}\:{median}\:{lengths}\:<\:{sum}\:{of}\:{sides}\:. \\ $$$$ \\ $$
Commented by Joel577 last updated on 25/May/17
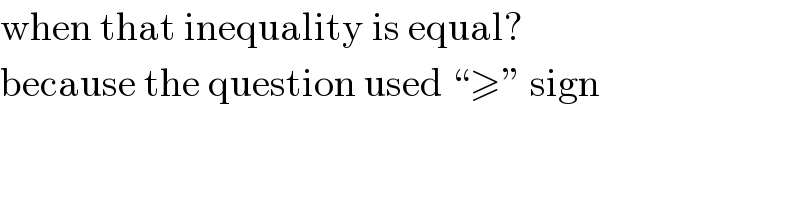
$$\mathrm{when}\:\mathrm{that}\:\mathrm{inequality}\:\mathrm{is}\:\mathrm{equal}? \\ $$$$\mathrm{because}\:\mathrm{the}\:\mathrm{question}\:\mathrm{used}\:``\geqslant''\:\mathrm{sign} \\ $$
Commented by ajfour last updated on 25/May/17
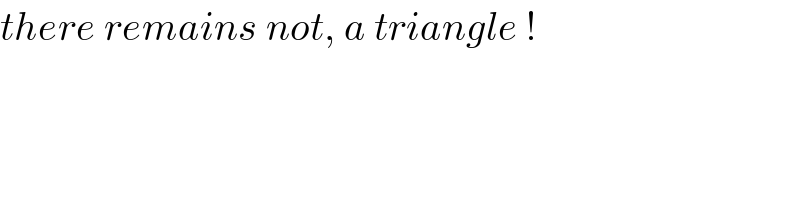
$${there}\:{remains}\:{not},\:{a}\:{triangle}\:! \\ $$
Commented by mrW1 last updated on 25/May/17
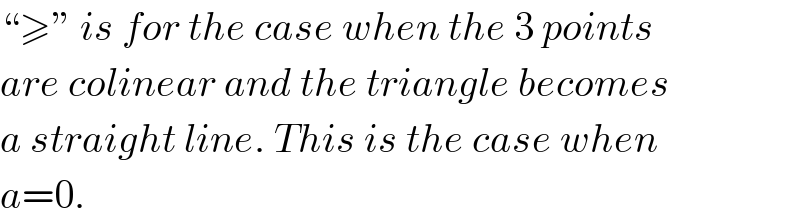
$$``\geqslant''\:{is}\:{for}\:{the}\:{case}\:{when}\:{the}\:\mathrm{3}\:{points} \\ $$$${are}\:{colinear}\:{and}\:{the}\:{triangle}\:{becomes} \\ $$$${a}\:{straight}\:{line}.\:{This}\:{is}\:{the}\:{case}\:{when} \\ $$$${a}=\mathrm{0}. \\ $$
