
Question Number 139285 by mohammad17 last updated on 25/Apr/21
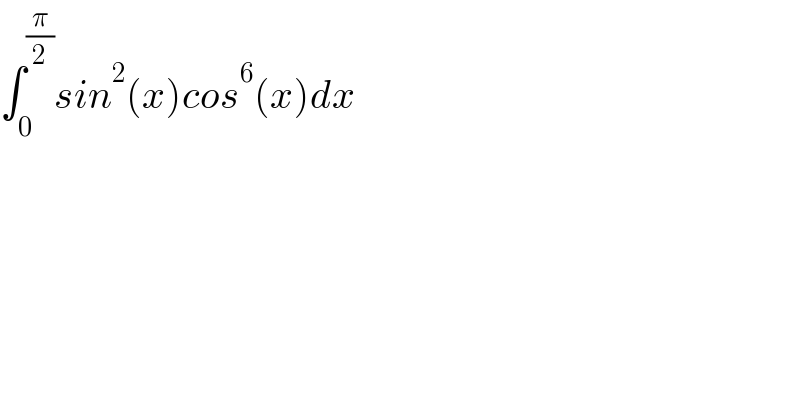
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}} \left({x}\right){cos}^{\mathrm{6}} \left({x}\right){dx} \\ $$
Answered by qaz last updated on 25/Apr/21
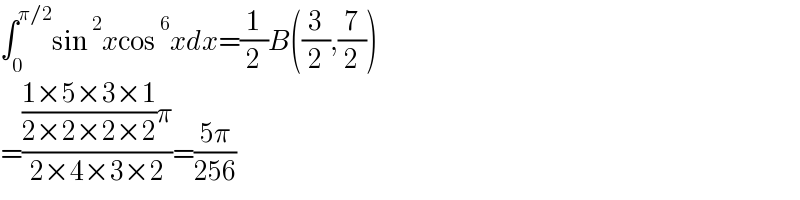
$$\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} {x}\mathrm{cos}\:^{\mathrm{6}} {xdx}=\frac{\mathrm{1}}{\mathrm{2}}{B}\left(\frac{\mathrm{3}}{\mathrm{2}},\frac{\mathrm{7}}{\mathrm{2}}\right) \\ $$$$=\frac{\frac{\mathrm{1}×\mathrm{5}×\mathrm{3}×\mathrm{1}}{\mathrm{2}×\mathrm{2}×\mathrm{2}×\mathrm{2}}\pi}{\mathrm{2}×\mathrm{4}×\mathrm{3}×\mathrm{2}}=\frac{\mathrm{5}\pi}{\mathrm{256}} \\ $$
Commented by mohammad17 last updated on 25/Apr/21
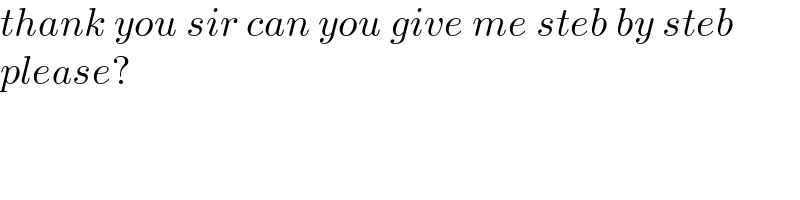
$${thank}\:{you}\:{sir}\:{can}\:{you}\:{give}\:{me}\:{steb}\:{by}\:{steb} \\ $$$${please}? \\ $$
Commented by qaz last updated on 25/Apr/21
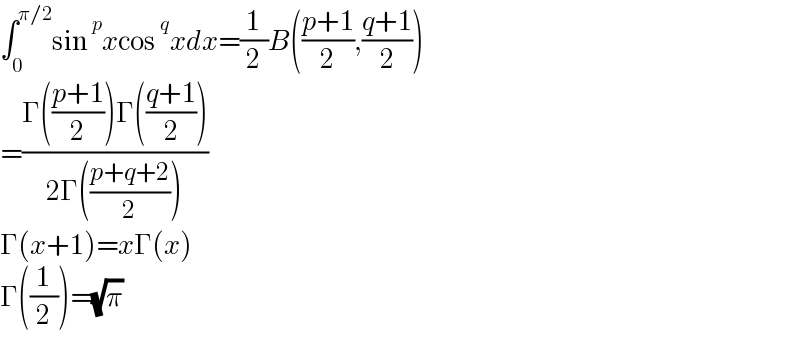
$$\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{sin}\:^{{p}} {x}\mathrm{cos}\:^{{q}} {xdx}=\frac{\mathrm{1}}{\mathrm{2}}{B}\left(\frac{{p}+\mathrm{1}}{\mathrm{2}},\frac{{q}+\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\frac{\Gamma\left(\frac{{p}+\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{{q}+\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}\Gamma\left(\frac{{p}+{q}+\mathrm{2}}{\mathrm{2}}\right)} \\ $$$$\Gamma\left({x}+\mathrm{1}\right)={x}\Gamma\left({x}\right) \\ $$$$\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\sqrt{\pi} \\ $$
Answered by MJS_new last updated on 25/Apr/21
![∫sin^2 x cos^6 x dx= [t=tan x → dx=cos^2 x dt] =∫(t^2 /((t^2 +1)^5 ))dt= [Ostrogradski′s Method] =((t(15t^6 +55t^4 +73t^2 −15))/(384(t^2 +1)^4 ))+(5/(128))∫(dt/(t^2 +1))= =((t(15t^6 +55t^4 +73t^2 −15))/(384(t^2 +1)^4 ))+(5/(128))arctan t ⇒ answer is ((5π)/(256))](Q139314.png)
$$\int\mathrm{sin}^{\mathrm{2}} \:{x}\:\mathrm{cos}^{\mathrm{6}} \:{x}\:{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:{x}\:\rightarrow\:{dx}=\mathrm{cos}^{\mathrm{2}} \:{x}\:{dt}\right] \\ $$$$=\int\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{5}} }{dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\right] \\ $$$$=\frac{{t}\left(\mathrm{15}{t}^{\mathrm{6}} +\mathrm{55}{t}^{\mathrm{4}} +\mathrm{73}{t}^{\mathrm{2}} −\mathrm{15}\right)}{\mathrm{384}\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{4}} }+\frac{\mathrm{5}}{\mathrm{128}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}= \\ $$$$=\frac{{t}\left(\mathrm{15}{t}^{\mathrm{6}} +\mathrm{55}{t}^{\mathrm{4}} +\mathrm{73}{t}^{\mathrm{2}} −\mathrm{15}\right)}{\mathrm{384}\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{4}} }+\frac{\mathrm{5}}{\mathrm{128}}\mathrm{arctan}\:{t} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{5}\pi}{\mathrm{256}} \\ $$
