
Question Number 139259 by bobhans last updated on 25/Apr/21
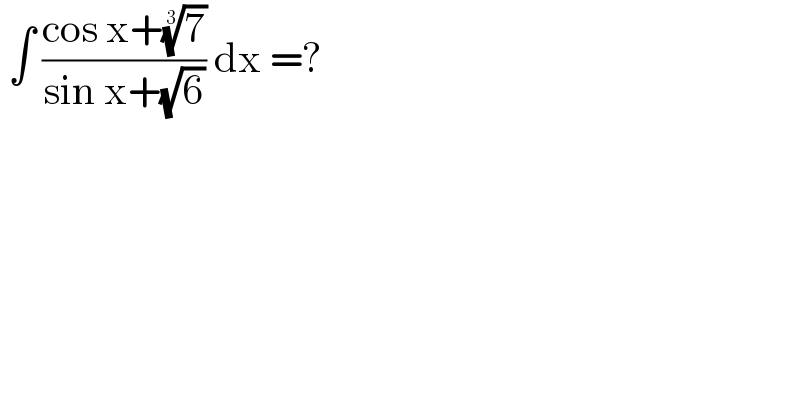
$$\:\int\:\frac{\mathrm{cos}\:\mathrm{x}+\sqrt[{\mathrm{3}}]{\mathrm{7}}}{\mathrm{sin}\:\mathrm{x}+\sqrt{\mathrm{6}}}\:\mathrm{dx}\:=? \\ $$
Answered by Dwaipayan Shikari last updated on 25/Apr/21
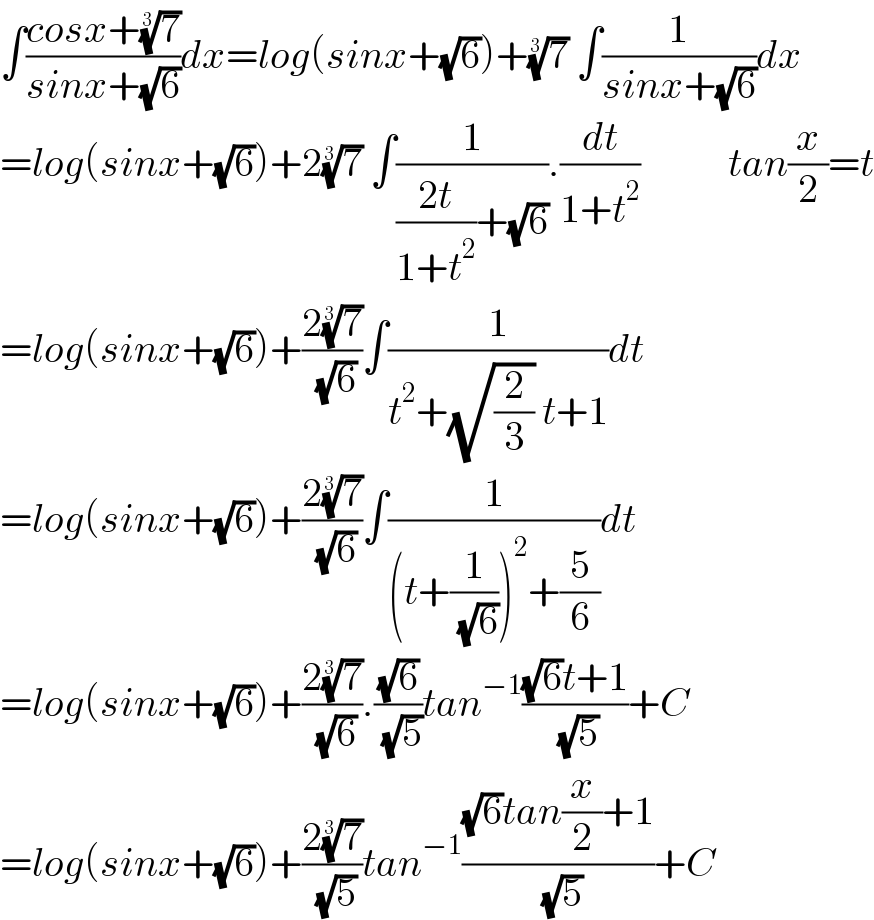
$$\int\frac{{cosx}+\sqrt[{\mathrm{3}}]{\mathrm{7}}}{{sinx}+\sqrt{\mathrm{6}}}{dx}={log}\left({sinx}+\sqrt{\mathrm{6}}\right)+\sqrt[{\mathrm{3}}]{\mathrm{7}}\:\int\frac{\mathrm{1}}{{sinx}+\sqrt{\mathrm{6}}}{dx} \\ $$$$={log}\left({sinx}+\sqrt{\mathrm{6}}\right)+\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{7}}\:\int\frac{\mathrm{1}}{\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }+\sqrt{\mathrm{6}}}.\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:\:\:{tan}\frac{{x}}{\mathrm{2}}={t} \\ $$$$={log}\left({sinx}+\sqrt{\mathrm{6}}\right)+\frac{\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{7}}}{\:\sqrt{\mathrm{6}}}\int\frac{\mathrm{1}}{{t}^{\mathrm{2}} +\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}\:{t}+\mathrm{1}}{dt} \\ $$$$={log}\left({sinx}+\sqrt{\mathrm{6}}\right)+\frac{\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{7}}}{\:\sqrt{\mathrm{6}}}\int\frac{\mathrm{1}}{\left({t}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}\right)^{\mathrm{2}} +\frac{\mathrm{5}}{\mathrm{6}}}{dt} \\ $$$$={log}\left({sinx}+\sqrt{\mathrm{6}}\right)+\frac{\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{7}}}{\:\sqrt{\mathrm{6}}}.\frac{\sqrt{\mathrm{6}}}{\:\sqrt{\mathrm{5}}}{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{6}}{t}+\mathrm{1}}{\:\sqrt{\mathrm{5}}}+{C} \\ $$$$={log}\left({sinx}+\sqrt{\mathrm{6}}\right)+\frac{\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{7}}}{\:\sqrt{\mathrm{5}}}{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{6}}{tan}\frac{{x}}{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{5}}}+{C} \\ $$
