
Question Number 139116 by EnterUsername last updated on 22/Apr/21
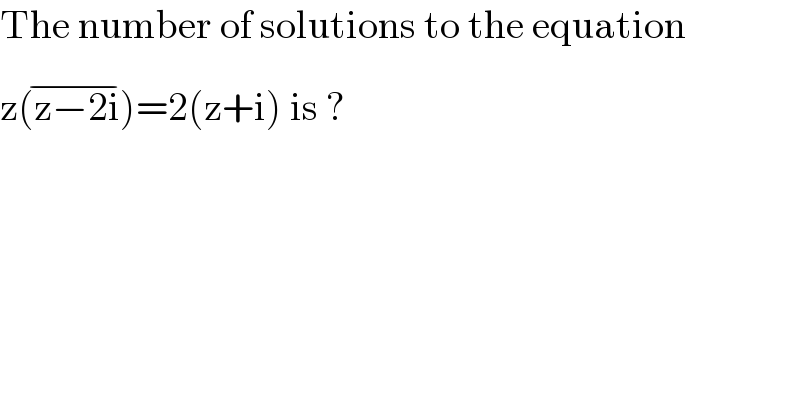
$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{solutions}\:\mathrm{to}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{z}\overline {\left(\mathrm{z}−\mathrm{2i}\right)}=\mathrm{2}\left(\mathrm{z}+\mathrm{i}\right)\:\mathrm{is}\:? \\ $$
Answered by qaz last updated on 22/Apr/21
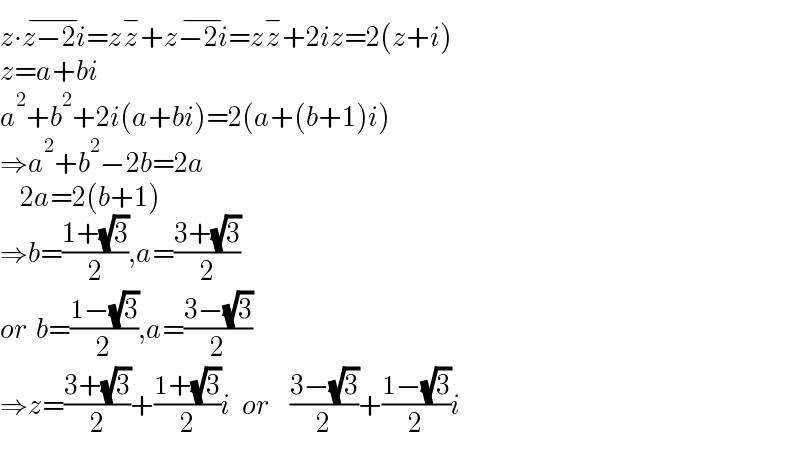
$${z}\centerdot\overline {{z}−\mathrm{2}{i}}={z}\overset{−} {{z}}+{z}\overline {−\mathrm{2}{i}}={z}\overset{−} {{z}}+\mathrm{2}{iz}=\mathrm{2}\left({z}+{i}\right) \\ $$$${z}={a}+{bi} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{i}\left({a}+{bi}\right)=\mathrm{2}\left({a}+\left({b}+\mathrm{1}\right){i}\right) \\ $$$$\Rightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{b}=\mathrm{2}{a} \\ $$$$\:\:\:\:\:\mathrm{2}{a}=\mathrm{2}\left({b}+\mathrm{1}\right) \\ $$$$\Rightarrow{b}=\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{2}},{a}=\frac{\mathrm{3}+\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${or}\:\:{b}=\frac{\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{2}},{a}=\frac{\mathrm{3}−\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\Rightarrow{z}=\frac{\mathrm{3}+\sqrt{\mathrm{3}}}{\mathrm{2}}+\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{2}}{i}\:\:\:{or}\:\:\:\:\:\frac{\mathrm{3}−\sqrt{\mathrm{3}}}{\mathrm{2}}+\frac{\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{2}}{i} \\ $$
