
Question Number 139105 by mnjuly1970 last updated on 22/Apr/21
Answered by bramlexs22 last updated on 22/Apr/21

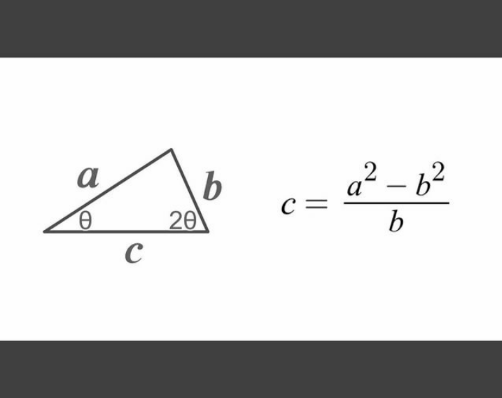
$$\frac{\mathrm{b}}{\mathrm{sin}\:\theta}=\frac{\mathrm{a}}{\mathrm{sin}\:\mathrm{2}\theta}\:\Rightarrow\:\mathrm{b}=\frac{\mathrm{a}}{\mathrm{2cos}\:\theta}\:;\:\mathrm{cos}\:\theta=\frac{\mathrm{a}}{\mathrm{2b}} \\ $$$$\measuredangle\mathrm{C}\:=\gamma=\:\mathrm{180}°−\mathrm{3}\theta \\ $$$$\mathrm{c}^{\mathrm{2}} \:=\:\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{2ab}\:\mathrm{cos}\:\gamma \\ $$$$\left(\bullet\right)\mathrm{cos}\:\gamma=−\mathrm{cos}\:\mathrm{3}\theta \\ $$$$\mathrm{c}=\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{2abcos}\:\mathrm{3}\theta} \\ $$$$\mathrm{cos}\:\mathrm{3}\theta=\mathrm{cos}\:\mathrm{2}\theta\mathrm{cos}\:\theta−\mathrm{sin}\:\mathrm{2}\theta\mathrm{sin}\:\theta \\ $$$$=\mathrm{cos}\:\theta\left(\mathrm{2cos}\:^{\mathrm{2}} \theta−\mathrm{1}\right)−\mathrm{2cos}\:\theta\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \theta\right) \\ $$$$=\mathrm{4cos}\:^{\mathrm{3}} \theta−\mathrm{3cos}\:\theta \\ $$$$=\mathrm{4}\left(\frac{\mathrm{a}^{\mathrm{3}} }{\mathrm{8b}^{\mathrm{3}} }\right)−\mathrm{3}\left(\frac{\mathrm{a}}{\mathrm{2b}}\right)=\frac{\mathrm{a}^{\mathrm{3}} }{\mathrm{2b}^{\mathrm{3}} }−\frac{\mathrm{3ab}^{\mathrm{2}} }{\mathrm{2b}^{\mathrm{3}} }=\frac{\mathrm{a}^{\mathrm{3}} −\mathrm{3ab}^{\mathrm{2}} }{\mathrm{2b}^{\mathrm{3}} } \\ $$$$\mathrm{c}\:=\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{2ab}\left(\frac{\mathrm{a}^{\mathrm{3}} −\mathrm{3ab}^{\mathrm{2}} }{\mathrm{2b}^{\mathrm{3}} }\right)} \\ $$$$=\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\frac{\mathrm{a}\left(\mathrm{a}^{\mathrm{3}} −\mathrm{3ab}^{\mathrm{2}} \right)}{\mathrm{b}^{\mathrm{2}} }} \\ $$$$=\frac{\sqrt{\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} +\mathrm{b}^{\mathrm{4}} +\mathrm{a}^{\mathrm{4}} −\mathrm{3a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} }}{\mathrm{b}} \\ $$$$=\frac{\sqrt{\mathrm{a}^{\mathrm{4}} +\mathrm{b}^{\mathrm{4}} −\mathrm{2a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} }}{\mathrm{b}}=\frac{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }{\mathrm{b}} \\ $$
Commented by mnjuly1970 last updated on 22/Apr/21
$${thanks}\:{alot}\:{master}... \\ $$
