
Question Number 139092 by mathdanisur last updated on 22/Apr/21
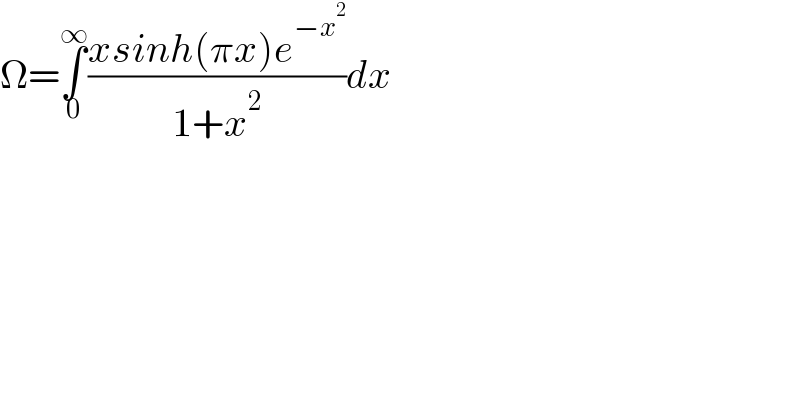
$$\Omega=\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{xsinh}\left(\pi{x}\right){e}^{−{x}^{\mathrm{2}} } }{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$
Answered by mathmax by abdo last updated on 23/Apr/21

$$\mathrm{i}\:\mathrm{give}\:\mathrm{this}\:\mathrm{soution}\:\mathrm{but}\:\mathrm{not}\:\mathrm{sure}! \\ $$$$\Phi=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{xsh}\left(\pi\mathrm{x}\right)\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } }{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:\Rightarrow\Phi=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \:\frac{\mathrm{xsh}\left(\pi\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{dx} \\ $$$$\mathrm{w}\left(\mathrm{z}\right)=\frac{\mathrm{zsh}\left(\pi\mathrm{z}\right)\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } }{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\mathrm{w}\left(\mathrm{z}\right)=\frac{\mathrm{zsh}\left(\pi\mathrm{z}\right)\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } }{\left(\mathrm{z}−\mathrm{i}\right)\left(\mathrm{z}+\mathrm{i}\right)} \\ $$$$\int_{−\infty} ^{+\infty} \:\mathrm{w}\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\mathrm{Res}\left(\mathrm{w},\mathrm{i}\right)\left[=\mathrm{2i}\pi×\frac{\mathrm{ish}\left(\pi\mathrm{i}\right)\mathrm{e}^{−\left(−\mathrm{1}\right)} }{\mathrm{2i}}=\mathrm{i}\pi\mathrm{sh}\left(\pi\mathrm{i}\right)\mathrm{e}\right. \\ $$$$\mathrm{but}\:\:\mathrm{sh}\left(\pi\mathrm{i}\right)=\frac{\mathrm{e}^{\mathrm{i}\left(\pi\mathrm{i}\right)} −\mathrm{e}^{−\mathrm{i}\left(\pi\mathrm{i}\right)} }{\mathrm{2i}}=\frac{\mathrm{e}^{−\pi} −\mathrm{e}^{\pi} }{\mathrm{2i}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\mathrm{w}\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{i}\pi\left(\frac{\mathrm{e}^{−\pi} −\mathrm{e}^{\pi} }{\mathrm{2i}}\right)\mathrm{e}\:=\pi\left(\mathrm{e}^{\mathrm{1}−\pi} −\mathrm{e}^{\mathrm{1}+\pi} \right)\:\Rightarrow \\ $$$$\Phi=\frac{\pi}{\mathrm{2}}\left(\mathrm{e}^{\mathrm{1}−\pi} −\mathrm{e}^{\mathrm{1}+\pi} \right) \\ $$
Commented by mathdanisur last updated on 23/Apr/21
$${thaks}\:{thanks}\:{Sir} \\ $$
Commented by mathdanisur last updated on 23/Apr/21
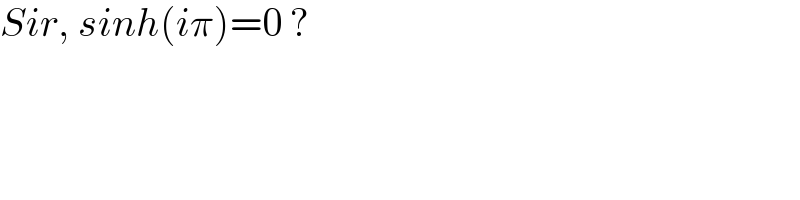
$${Sir},\:{sinh}\left({i}\pi\right)=\mathrm{0}\:? \\ $$
Commented by mathmax by abdo last updated on 24/Apr/21
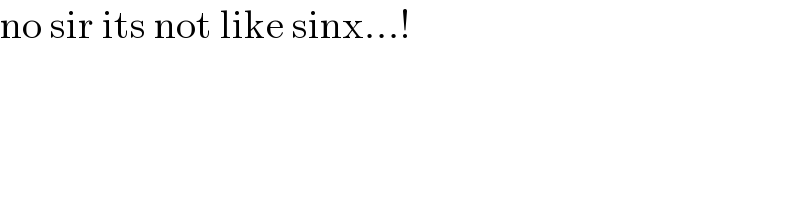
$$\mathrm{no}\:\mathrm{sir}\:\mathrm{its}\:\mathrm{not}\:\mathrm{like}\:\mathrm{sinx}...! \\ $$
Commented by mathdanisur last updated on 24/Apr/21
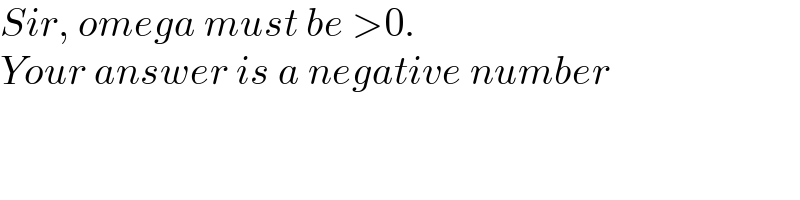
$${Sir},\:{omega}\:{must}\:{be}\:>\mathrm{0}. \\ $$$${Your}\:{answer}\:{is}\:{a}\:{negative}\:{number} \\ $$
Commented by mathdanisur last updated on 24/Apr/21
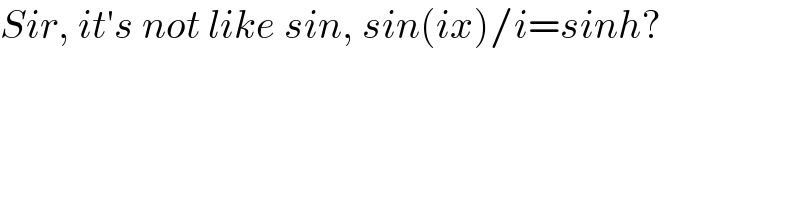
$${Sir},\:{it}'{s}\:{not}\:{like}\:{sin},\:{sin}\left({ix}\right)/{i}={sinh}? \\ $$
