
Question Number 139036 by mnjuly1970 last updated on 21/Apr/21
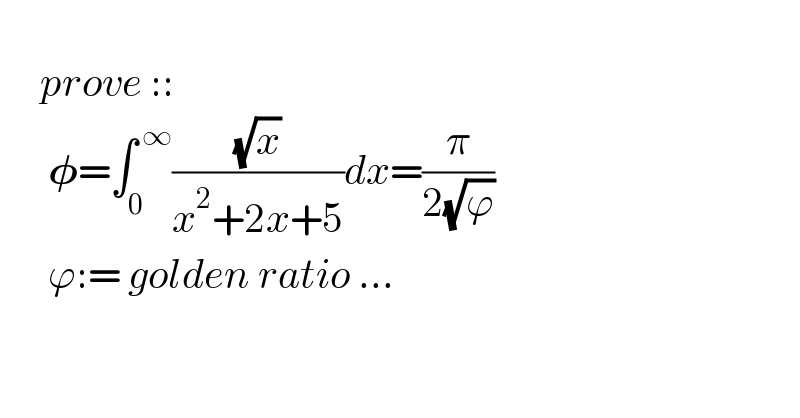
$$\:\:\:\: \\ $$$$\:\:\:\:\:{prove}\::: \\ $$$$\:\:\:\:\:\:\boldsymbol{\phi}=\int_{\mathrm{0}} ^{\:\infty} \frac{\sqrt{{x}}}{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{5}}{dx}=\frac{\pi}{\mathrm{2}\sqrt{\varphi}} \\ $$$$\:\:\:\:\:\:\varphi:=\:{golden}\:{ratio}\:... \\ $$
Answered by Dwaipayan Shikari last updated on 21/Apr/21

$$\frac{\mathrm{1}}{\mathrm{4}{i}}\int_{\mathrm{0}} ^{\infty} \frac{\sqrt{{x}}}{\left({x}+\mathrm{1}−\mathrm{2}{i}\right)}−\frac{\sqrt{{x}}}{\left({x}+\mathrm{1}+\mathrm{2}{i}\right)}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{i}}−\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} +\mathrm{1}+\mathrm{2}{i}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2}{i}−\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{i}}+\frac{\mathrm{2}{i}+\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}+\mathrm{2}{i}}{dt}=\frac{\pi}{\mathrm{4}{i}}\left(\frac{\mathrm{2}{i}−\mathrm{1}}{\:\sqrt{\mathrm{1}−\mathrm{2}{i}}}+\frac{\mathrm{2}{i}+\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{2}{i}}}\right) \\ $$$$=\frac{\pi}{\mathrm{4}{i}}\left(−\sqrt{\mathrm{1}−\mathrm{2}{i}}+\sqrt{\mathrm{1}+\mathrm{2}{i}}\right)=\frac{\pi}{\mathrm{4}{i}}\left(\mathrm{2}{i}\sqrt{\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}}\right)=\frac{\pi}{\mathrm{2}\sqrt{\varphi}} \\ $$$$== \\ $$$$\sqrt{{x}+\sqrt{−{y}}}=\sqrt{\frac{{x}+\sqrt{{x}^{\mathrm{2}} +{y}}}{\mathrm{2}}}+\sqrt{\frac{{x}−\sqrt{{x}^{\mathrm{2}} +{y}}}{\mathrm{2}}} \\ $$$$\sqrt{{x}−\sqrt{−{y}}}=\sqrt{\frac{{x}+\sqrt{{x}^{\mathrm{2}} +{y}}}{\mathrm{2}}}−\sqrt{\frac{{x}−\sqrt{{x}^{\mathrm{2}} +{y}}}{\mathrm{2}}} \\ $$$$\sqrt{\mathrm{1}+\mathrm{2}{i}}=\sqrt{\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}}+{i}\sqrt{\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}} \\ $$$$\sqrt{\mathrm{1}−\mathrm{2}{i}}=\sqrt{\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}}−{i}\sqrt{\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}} \\ $$
Commented by mnjuly1970 last updated on 21/Apr/21

$${thanks}\:{alot}... \\ $$
Answered by mnjuly1970 last updated on 21/Apr/21

Answered by mathmax by abdo last updated on 21/Apr/21

$$\Phi=\int_{\mathrm{0}} ^{\infty} \:\frac{\sqrt{\mathrm{x}}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{5}}\mathrm{dx}\:\Rightarrow\Phi=_{\sqrt{\mathrm{x}}=\mathrm{t}} \:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}\left(\mathrm{2t}\right)}{\mathrm{t}^{\mathrm{4}} \:+\mathrm{2t}^{\mathrm{2}} \:+\mathrm{5}}\mathrm{dt} \\ $$$$=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{4}} \:+\mathrm{2t}^{\mathrm{2}} \:+\mathrm{5}}\mathrm{dt}\:\:\mathrm{let}\:\mathrm{w}\left(\mathrm{z}\right)=\frac{\mathrm{z}^{\mathrm{2}} }{\mathrm{z}^{\mathrm{4}} \:+\mathrm{2z}^{\mathrm{2}} \:+\mathrm{5}}\:\:\mathrm{poles}\:\mathrm{of}\:\mathrm{w}! \\ $$$$\mathrm{z}^{\mathrm{4}} \:+\mathrm{2z}^{\mathrm{2}} \:+\mathrm{5}=\mathrm{0}\:\rightarrow\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{5}=\mathrm{0}\left(\mathrm{t}^{\mathrm{2}} =\mathrm{x}\right) \\ $$$$\Delta=\mathrm{4}−\mathrm{20}=−\mathrm{16}\:\Rightarrow\mathrm{x}_{\mathrm{1}} =\frac{−\mathrm{2}+\mathrm{i}\sqrt{\mathrm{20}}}{\mathrm{2}}\:=\frac{−\mathrm{2}+\mathrm{2i}\sqrt{\mathrm{5}}}{\mathrm{2}}=−\mathrm{1}+\mathrm{i}\sqrt{\mathrm{5}} \\ $$$$\mathrm{x}_{\mathrm{2}} =−\mathrm{1}−\mathrm{i}\sqrt{\mathrm{5}}\:\Rightarrow\:\mathrm{w}\left(\mathrm{z}\right)=\frac{\mathrm{z}^{\mathrm{2}} }{\left(\mathrm{z}^{\mathrm{2}} +\mathrm{1}−\mathrm{i}\sqrt{\mathrm{5}}\right)\left(\mathrm{z}^{\mathrm{2}} +\mathrm{1}+\mathrm{i}\sqrt{\mathrm{5}}\right)} \\ $$$$=\frac{\mathrm{z}^{\mathrm{2}} }{\left(\mathrm{z}−\sqrt{\mathrm{x}_{\mathrm{1}} }\right)\left(\mathrm{z}+\sqrt{\mathrm{x}_{\mathrm{1}} }\right)\left(\mathrm{z}−\sqrt{\mathrm{x}_{\mathrm{2}} }\right)\left(\mathrm{z}+\sqrt{\mathrm{x}_{\mathrm{2}} }\right)} \\ $$$$\mathrm{x}_{\mathrm{1}} =\sqrt{\mathrm{6}}\mathrm{e}^{−\mathrm{iarctan}\left(\sqrt{\mathrm{5}}\right)} \:\:\:\mathrm{and}\:\mathrm{x}_{\mathrm{2}} =\sqrt{\mathrm{6}}\mathrm{e}^{\mathrm{iarctan}\left(\sqrt{\mathrm{5}}\right)} \\ $$$$\Rightarrow\mathrm{w}\left(\mathrm{z}\right)=\frac{\mathrm{z}^{\mathrm{2}} }{\left(\mathrm{z}−\sqrt{\sqrt{\mathrm{6}}}\mathrm{e}^{−\frac{\mathrm{i}}{\mathrm{2}}\mathrm{arctan}\left(\sqrt{\mathrm{5}}\right)} \right)\left(\mathrm{z}+\sqrt{\sqrt{\mathrm{6}}}\mathrm{e}^{−\frac{\mathrm{i}}{\mathrm{2}}\mathrm{arctan}\left(\sqrt{\mathrm{5}}\right)} \right)\left(\mathrm{z}−\sqrt{\sqrt{\mathrm{6}}}\mathrm{e}^{\frac{\mathrm{i}}{\mathrm{2}}\mathrm{arctan}\left(\sqrt{\mathrm{5}}\right)} \right)\left(\mathrm{z}+\sqrt{\sqrt{\mathrm{6}}}\mathrm{e}^{\frac{\mathrm{i}}{\mathrm{2}}\mathrm{arctan}\left(\sqrt{\mathrm{5}}\right)} \right)} \\ $$$$\int_{−\infty} ^{+\infty} \:\mathrm{w}\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\left\{\:\mathrm{Res}\left(\mathrm{w},−\sqrt{\sqrt{\mathrm{6}}}\mathrm{e}^{−\frac{\mathrm{i}}{\mathrm{2}}\mathrm{arctan}\left(\sqrt{\mathrm{5}}\right)} \:+\mathrm{Res}\left(\mathrm{w},\sqrt{\sqrt{\mathrm{6}}}\mathrm{e}^{\frac{\mathrm{i}}{\mathrm{2}}\mathrm{arctan}\left(\sqrt{\mathrm{5}}\right)} \right\}\right.\right. \\ $$$$\mathrm{Res}\left(\mathrm{w},\sqrt{\sqrt{\mathrm{6}}}\mathrm{e}^{\frac{\mathrm{i}}{\mathrm{2}}\mathrm{arctan}\left(\sqrt{\mathrm{5}}\right)} \right)\:=\frac{\sqrt{\mathrm{6}}\mathrm{e}^{\mathrm{iarctan}\left(\sqrt{\mathrm{5}}\right)} }{\mathrm{2}\sqrt{\sqrt{\mathrm{6}}}\mathrm{e}^{\frac{\mathrm{i}}{\mathrm{2}}\mathrm{arctan}\left(\sqrt{\mathrm{5}}\right)} \sqrt{\mathrm{6}}\left(\mathrm{2isin}\left(\mathrm{arctan}\left(\sqrt{\mathrm{5}}\right)\right.\right.} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4i}}\frac{\mathrm{e}^{\frac{\mathrm{i}}{\mathrm{2}}\mathrm{arctan}\left(\sqrt{\mathrm{5}}\right)} }{\:\sqrt{\sqrt{\mathrm{6}}}\mathrm{sin}\left(\mathrm{arctan}\left(\sqrt{\mathrm{5}}\right)\right)}....\mathrm{be}\:\mathrm{continued}... \\ $$
