
Question Number 138989 by metamorfose last updated on 20/Apr/21
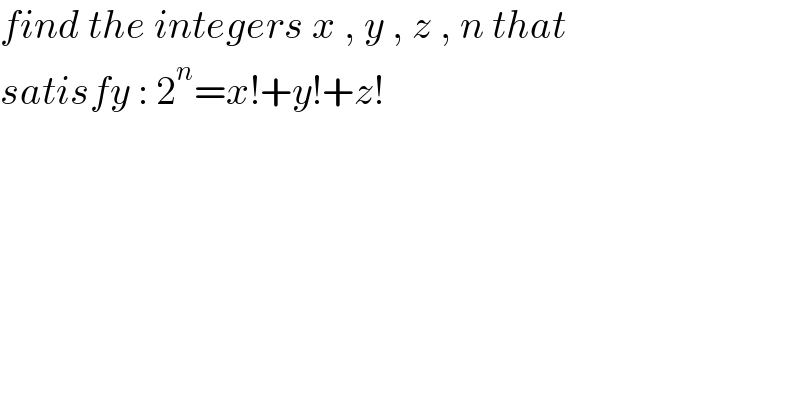
$${find}\:{the}\:{integers}\:{x}\:,\:{y}\:,\:{z}\:,\:{n}\:{that} \\ $$$${satisfy}\::\:\mathrm{2}^{{n}} ={x}!+{y}!+{z}! \\ $$
Answered by mindispower last updated on 21/Apr/21
![let m=min(x,y,z),if m≥3⇒ x!+y!+z!≡0[3]⇔2^n ≡0[3] impossib since 2,3 are coprime ⇒m∈{0,1,2} by symetrie of x!+y!+z! let m=x,x≤y≤z x=0,1⇒2^n −1=z!+y!≥2⇒n≥2 z!+y!≡1[2]⇒y={0,1} ⇒2^n −2=z!⇒2(2^(n−1) −1)=z!,we see z≥2 since 2∣2(2^(n−1) −1) the power of 2 in the 2(2^(n−1) −1)is one since 2^(n−1) −1≡1[2]⇒z<4⇒z∈{2,3} z=2⇒2^n −2=2⇒n=2 z=3⇒2^n =8⇒n=3 case 2 x=2 ⇒2^n −2=y!+z!⇒2(2^(n−1) −1)=y!+z!,2≤y<4 because power of 2 in 2(2^(n−1) −1)=1 and y≤z if y≥4⇒4∣(y!+z!) ⇒power of 2 in y!+z! is at less 2 impossibl if y=2 ⇒2^2 (2^(n−2) −1)=z!⇒no solution y=3⇒2(2^(n−1) −1)=6+z! ⇒2^3 (2^(n−3) −1)=z!⇒z={4,5} z=4⇒24=2^n −8⇒n=5 z=5⇒128=2^n ⇒n=7,ander permutation of x,y,z](Q139019.png)
$${let}\:{m}={min}\left({x},{y},{z}\right),{if}\:{m}\geqslant\mathrm{3}\Rightarrow \\ $$$${x}!+{y}!+{z}!\equiv\mathrm{0}\left[\mathrm{3}\right]\Leftrightarrow\mathrm{2}^{{n}} \equiv\mathrm{0}\left[\mathrm{3}\right]\:{impossib}\:{since} \\ $$$$\mathrm{2},\mathrm{3}\:{are}\:{coprime} \\ $$$$\Rightarrow{m}\in\left\{\mathrm{0},\mathrm{1},\mathrm{2}\right\}\:{by}\:{symetrie}\:{of}\:{x}!+{y}!+{z}! \\ $$$${let}\:{m}={x},{x}\leqslant{y}\leqslant{z} \\ $$$${x}=\mathrm{0},\mathrm{1}\Rightarrow\mathrm{2}^{{n}} −\mathrm{1}={z}!+{y}!\geqslant\mathrm{2}\Rightarrow{n}\geqslant\mathrm{2} \\ $$$${z}!+{y}!\equiv\mathrm{1}\left[\mathrm{2}\right]\Rightarrow{y}=\left\{\mathrm{0},\mathrm{1}\right\} \\ $$$$\Rightarrow\mathrm{2}^{{n}} −\mathrm{2}={z}!\Rightarrow\mathrm{2}\left(\mathrm{2}^{{n}−\mathrm{1}} −\mathrm{1}\right)={z}!,{we}\:{see}\:{z}\geqslant\mathrm{2} \\ $$$${since}\:\mathrm{2}\mid\mathrm{2}\left(\mathrm{2}^{{n}−\mathrm{1}} −\mathrm{1}\right) \\ $$$${the}\:{power}\:{of}\:\mathrm{2}\:{in}\:{the}\:\mathrm{2}\left(\mathrm{2}^{{n}−\mathrm{1}} −\mathrm{1}\right){is}\:{one}\:{since} \\ $$$$\mathrm{2}^{{n}−\mathrm{1}} −\mathrm{1}\equiv\mathrm{1}\left[\mathrm{2}\right]\Rightarrow{z}<\mathrm{4}\Rightarrow{z}\in\left\{\mathrm{2},\mathrm{3}\right\} \\ $$$${z}=\mathrm{2}\Rightarrow\mathrm{2}^{{n}} −\mathrm{2}=\mathrm{2}\Rightarrow{n}=\mathrm{2} \\ $$$${z}=\mathrm{3}\Rightarrow\mathrm{2}^{{n}} =\mathrm{8}\Rightarrow{n}=\mathrm{3} \\ $$$${case}\:\mathrm{2}\:{x}=\mathrm{2} \\ $$$$\Rightarrow\mathrm{2}^{{n}} −\mathrm{2}={y}!+{z}!\Rightarrow\mathrm{2}\left(\mathrm{2}^{{n}−\mathrm{1}} −\mathrm{1}\right)={y}!+{z}!,\mathrm{2}\leqslant{y}<\mathrm{4} \\ $$$${because}\:{power}\:{of}\:\mathrm{2}\:{in}\:\mathrm{2}\left(\mathrm{2}^{{n}−\mathrm{1}} −\mathrm{1}\right)=\mathrm{1} \\ $$$${and}\:{y}\leqslant{z}\:{if}\:{y}\geqslant\mathrm{4}\Rightarrow\mathrm{4}\mid\left({y}!+{z}!\right)\:\Rightarrow{power}\:{of}\:\mathrm{2}\:{in}\: \\ $$$${y}!+{z}!\:{is}\:{at}\:{less}\:\mathrm{2}\:{impossibl} \\ $$$${if}\:{y}=\mathrm{2} \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{2}} \left(\mathrm{2}^{{n}−\mathrm{2}} −\mathrm{1}\right)=\boldsymbol{{z}}!\Rightarrow{no}\:{solution} \\ $$$${y}=\mathrm{3}\Rightarrow\mathrm{2}\left(\mathrm{2}^{{n}−\mathrm{1}} −\mathrm{1}\right)=\mathrm{6}+{z}! \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{3}} \left(\mathrm{2}^{{n}−\mathrm{3}} −\mathrm{1}\right)={z}!\Rightarrow{z}=\left\{\mathrm{4},\mathrm{5}\right\} \\ $$$${z}=\mathrm{4}\Rightarrow\mathrm{24}=\mathrm{2}^{{n}} −\mathrm{8}\Rightarrow{n}=\mathrm{5} \\ $$$${z}=\mathrm{5}\Rightarrow\mathrm{128}=\mathrm{2}^{{n}} \Rightarrow{n}=\mathrm{7},{ander}\:{permutation}\: \\ $$$${of}\:{x},{y},{z} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by metamorfose last updated on 21/Apr/21

$${thnx}\:{sir} \\ $$
