
Question Number 138984 by bramlexs22 last updated on 20/Apr/21
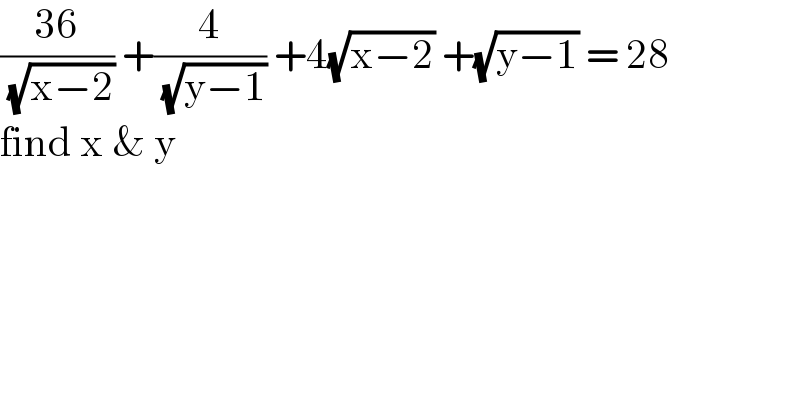
$$\frac{\mathrm{36}}{\:\sqrt{\mathrm{x}−\mathrm{2}}}\:+\frac{\mathrm{4}}{\:\sqrt{\mathrm{y}−\mathrm{1}}}\:+\mathrm{4}\sqrt{\mathrm{x}−\mathrm{2}}\:+\sqrt{\mathrm{y}−\mathrm{1}}\:=\:\mathrm{28} \\ $$ $$\mathrm{find}\:\mathrm{x}\:\&\:\mathrm{y} \\ $$
Answered by mitica last updated on 21/Apr/21
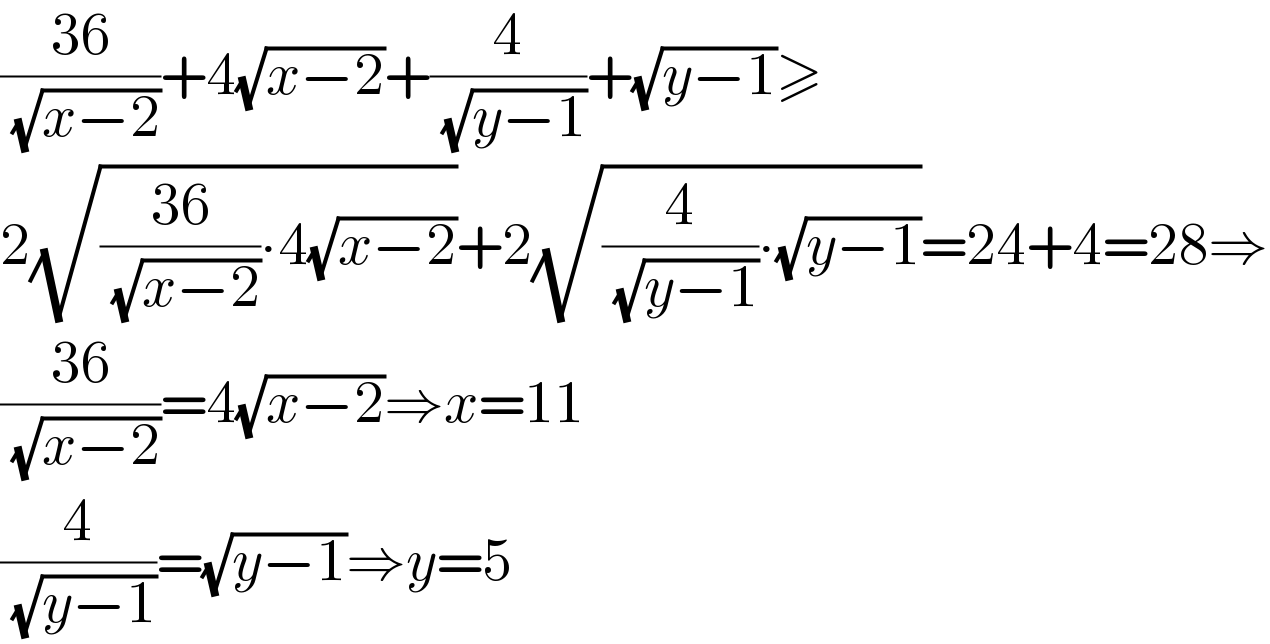
$$\frac{\mathrm{36}}{\:\sqrt{{x}−\mathrm{2}}}+\mathrm{4}\sqrt{{x}−\mathrm{2}}+\frac{\mathrm{4}}{\:\sqrt{{y}−\mathrm{1}}}+\sqrt{{y}−\mathrm{1}}\geqslant \\ $$ $$\mathrm{2}\sqrt{\frac{\mathrm{36}}{\:\sqrt{{x}−\mathrm{2}}}\centerdot\mathrm{4}\sqrt{{x}−\mathrm{2}}}+\mathrm{2}\sqrt{\frac{\mathrm{4}}{\:\sqrt{{y}−\mathrm{1}}}\centerdot\sqrt{{y}−\mathrm{1}}}=\mathrm{24}+\mathrm{4}=\mathrm{28}\Rightarrow \\ $$ $$\frac{\mathrm{36}}{\:\sqrt{{x}−\mathrm{2}}}=\mathrm{4}\sqrt{{x}−\mathrm{2}}\Rightarrow{x}=\mathrm{11} \\ $$ $$\frac{\mathrm{4}}{\:\sqrt{{y}−\mathrm{1}}}=\sqrt{{y}−\mathrm{1}}\Rightarrow{y}=\mathrm{5} \\ $$
Commented bybramlexs22 last updated on 21/Apr/21

$$\mathrm{AM}−\mathrm{GM} \\ $$
Answered by mr W last updated on 21/Apr/21
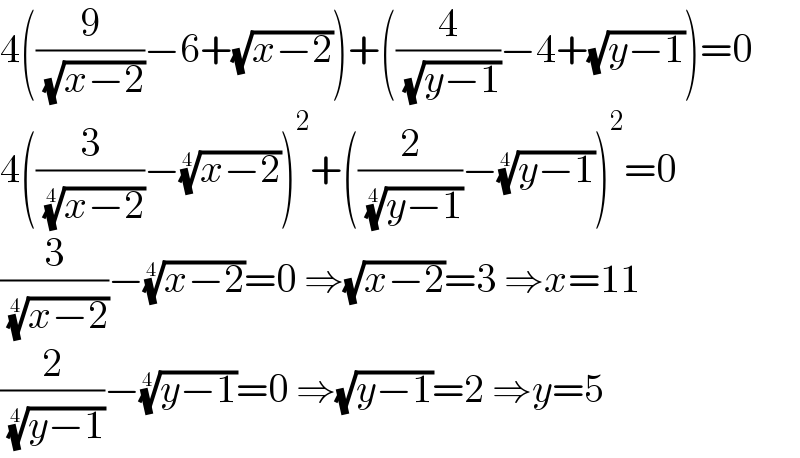
$$\mathrm{4}\left(\frac{\mathrm{9}}{\:\sqrt{{x}−\mathrm{2}}}−\mathrm{6}+\sqrt{{x}−\mathrm{2}}\right)+\left(\frac{\mathrm{4}}{\:\sqrt{{y}−\mathrm{1}}}−\mathrm{4}+\sqrt{{y}−\mathrm{1}}\right)=\mathrm{0} \\ $$ $$\mathrm{4}\left(\frac{\mathrm{3}}{\:\sqrt[{\mathrm{4}}]{{x}−\mathrm{2}}}−\sqrt[{\mathrm{4}}]{{x}−\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{2}}{\:\sqrt[{\mathrm{4}}]{{y}−\mathrm{1}}}−\sqrt[{\mathrm{4}}]{{y}−\mathrm{1}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$ $$\frac{\mathrm{3}}{\:\sqrt[{\mathrm{4}}]{{x}−\mathrm{2}}}−\sqrt[{\mathrm{4}}]{{x}−\mathrm{2}}=\mathrm{0}\:\Rightarrow\sqrt{{x}−\mathrm{2}}=\mathrm{3}\:\Rightarrow{x}=\mathrm{11} \\ $$ $$\frac{\mathrm{2}}{\:\sqrt[{\mathrm{4}}]{{y}−\mathrm{1}}}−\sqrt[{\mathrm{4}}]{{y}−\mathrm{1}}=\mathrm{0}\:\Rightarrow\sqrt{{y}−\mathrm{1}}=\mathrm{2}\:\Rightarrow{y}=\mathrm{5} \\ $$
