
Question Number 138872 by peter frank last updated on 19/Apr/21

Answered by bramlexs22 last updated on 19/Apr/21
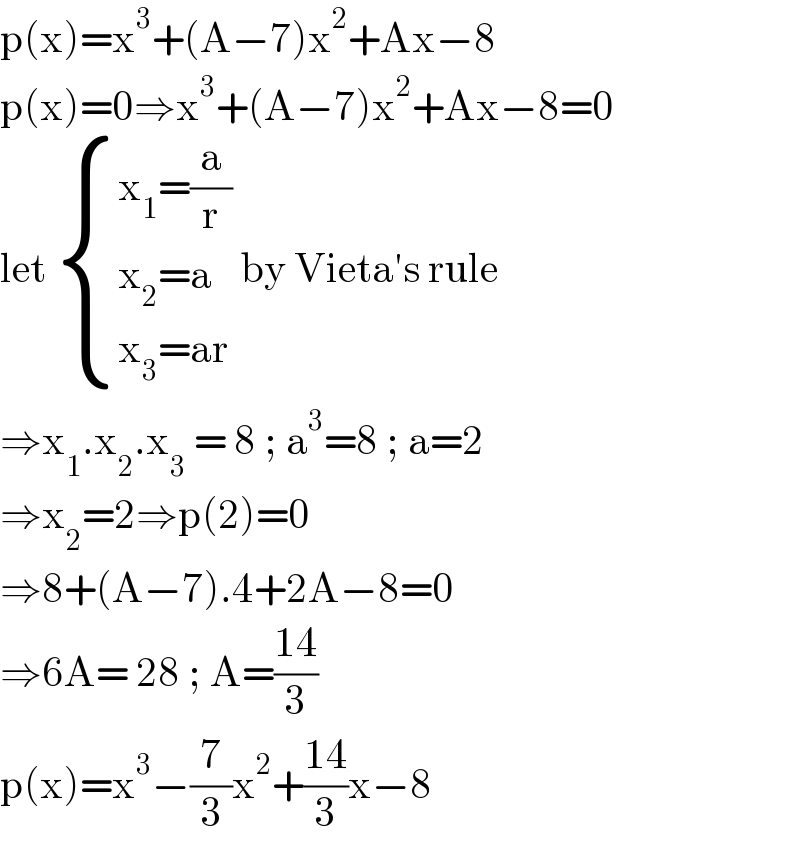
$$\mathrm{p}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{3}} +\left(\mathrm{A}−\mathrm{7}\right)\mathrm{x}^{\mathrm{2}} +\mathrm{Ax}−\mathrm{8} \\ $$$$\mathrm{p}\left(\mathrm{x}\right)=\mathrm{0}\Rightarrow\mathrm{x}^{\mathrm{3}} +\left(\mathrm{A}−\mathrm{7}\right)\mathrm{x}^{\mathrm{2}} +\mathrm{Ax}−\mathrm{8}=\mathrm{0} \\ $$$$\mathrm{let}\:\begin{cases}{\mathrm{x}_{\mathrm{1}} =\frac{\mathrm{a}}{\mathrm{r}}}\\{\mathrm{x}_{\mathrm{2}} =\mathrm{a}}\\{\mathrm{x}_{\mathrm{3}} =\mathrm{ar}}\end{cases}\:\mathrm{by}\:\mathrm{Vieta}'\mathrm{s}\:\mathrm{rule} \\ $$$$\Rightarrow\mathrm{x}_{\mathrm{1}} .\mathrm{x}_{\mathrm{2}} .\mathrm{x}_{\mathrm{3}} \:=\:\mathrm{8}\:;\:\mathrm{a}^{\mathrm{3}} =\mathrm{8}\:;\:\mathrm{a}=\mathrm{2} \\ $$$$\Rightarrow\mathrm{x}_{\mathrm{2}} =\mathrm{2}\Rightarrow\mathrm{p}\left(\mathrm{2}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{8}+\left(\mathrm{A}−\mathrm{7}\right).\mathrm{4}+\mathrm{2A}−\mathrm{8}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{6A}=\:\mathrm{28}\:;\:\mathrm{A}=\frac{\mathrm{14}}{\mathrm{3}} \\ $$$$\mathrm{p}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{3}} −\frac{\mathrm{7}}{\mathrm{3}}\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{14}}{\mathrm{3}}\mathrm{x}−\mathrm{8}\: \\ $$
Commented by peter frank last updated on 19/Apr/21
$${thank}\:{you} \\ $$
Answered by Rasheed.Sindhi last updated on 21/Apr/21
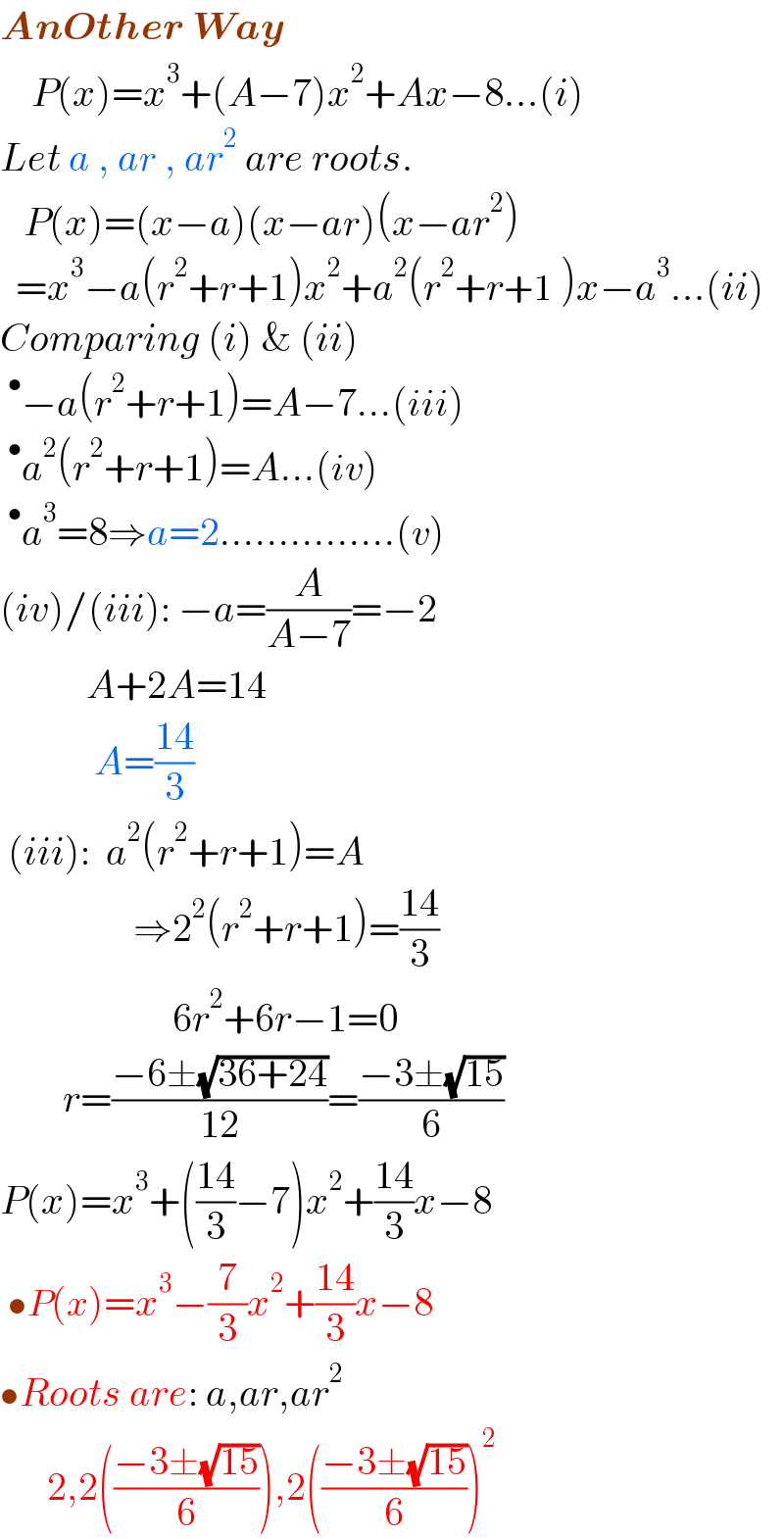
$$\boldsymbol{{AnOther}}\:\boldsymbol{{Way}} \\ $$$$\:\:\:\:{P}\left({x}\right)={x}^{\mathrm{3}} +\left({A}−\mathrm{7}\right){x}^{\mathrm{2}} +{Ax}−\mathrm{8}...\left({i}\right) \\ $$$${Let}\:{a}\:,\:{ar}\:,\:{ar}^{\mathrm{2}} \:{are}\:{roots}. \\ $$$$\:\:\:{P}\left({x}\right)=\left({x}−{a}\right)\left({x}−{ar}\right)\left({x}−{ar}^{\mathrm{2}} \right) \\ $$$$\:\:={x}^{\mathrm{3}} −{a}\left({r}^{\mathrm{2}} +{r}+\mathrm{1}\right){x}^{\mathrm{2}} +{a}^{\mathrm{2}} \left({r}^{\mathrm{2}} +{r}+\mathrm{1}\:\right){x}−{a}^{\mathrm{3}} ...\left({ii}\right) \\ $$$${Comparing}\:\left({i}\right)\:\&\:\left({ii}\right) \\ $$$$\:^{\bullet} −{a}\left({r}^{\mathrm{2}} +{r}+\mathrm{1}\right)={A}−\mathrm{7}...\left({iii}\right) \\ $$$$\:^{\bullet} {a}^{\mathrm{2}} \left({r}^{\mathrm{2}} +{r}+\mathrm{1}\right)={A}...\left({iv}\right) \\ $$$$\:^{\bullet} {a}^{\mathrm{3}} =\mathrm{8}\Rightarrow{a}=\mathrm{2}...............\left({v}\right) \\ $$$$\left({iv}\right)/\left({iii}\right):\:−{a}=\frac{{A}}{{A}−\mathrm{7}}=−\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{A}+\mathrm{2}{A}=\mathrm{14} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{A}=\frac{\mathrm{14}}{\mathrm{3}} \\ $$$$\:\left({iii}\right):\:\:{a}^{\mathrm{2}} \left({r}^{\mathrm{2}} +{r}+\mathrm{1}\right)={A} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{2}^{\mathrm{2}} \left({r}^{\mathrm{2}} +{r}+\mathrm{1}\right)=\frac{\mathrm{14}}{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{6}{r}^{\mathrm{2}} +\mathrm{6}{r}−\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:{r}=\frac{−\mathrm{6}\pm\sqrt{\mathrm{36}+\mathrm{24}}}{\mathrm{12}}=\frac{−\mathrm{3}\pm\sqrt{\mathrm{15}}}{\mathrm{6}} \\ $$$${P}\left({x}\right)={x}^{\mathrm{3}} +\left(\frac{\mathrm{14}}{\mathrm{3}}−\mathrm{7}\right){x}^{\mathrm{2}} +\frac{\mathrm{14}}{\mathrm{3}}{x}−\mathrm{8} \\ $$$$\:\bullet{P}\left({x}\right)={x}^{\mathrm{3}} −\frac{\mathrm{7}}{\mathrm{3}}{x}^{\mathrm{2}} +\frac{\mathrm{14}}{\mathrm{3}}{x}−\mathrm{8} \\ $$$$\bullet{Roots}\:{are}:\:{a},{ar},{ar}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\mathrm{2},\mathrm{2}\left(\frac{−\mathrm{3}\pm\sqrt{\mathrm{15}}}{\mathrm{6}}\right),\mathrm{2}\left(\frac{−\mathrm{3}\pm\sqrt{\mathrm{15}}}{\mathrm{6}}\right)^{\mathrm{2}} \\ $$
Commented by peter frank last updated on 12/May/21

$${thank}\:{you} \\ $$
