
Question Number 138827 by mathdanisur last updated on 18/Apr/21
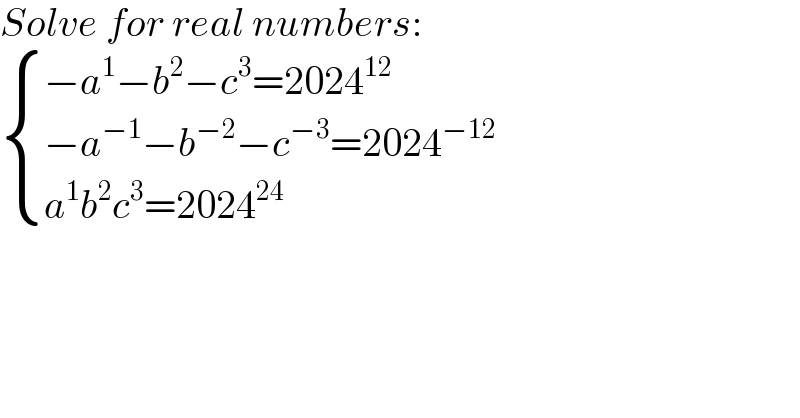
$${Solve}\:{for}\:{real}\:{numbers}: \\ $$$$\begin{cases}{−{a}^{\mathrm{1}} −{b}^{\mathrm{2}} −{c}^{\mathrm{3}} =\mathrm{2024}^{\mathrm{12}} }\\{−{a}^{−\mathrm{1}} −{b}^{−\mathrm{2}} −{c}^{−\mathrm{3}} =\mathrm{2024}^{−\mathrm{12}} }\\{{a}^{\mathrm{1}} {b}^{\mathrm{2}} {c}^{\mathrm{3}} =\mathrm{2024}^{\mathrm{24}} }\end{cases} \\ $$
Answered by MJS_new last updated on 18/Apr/21
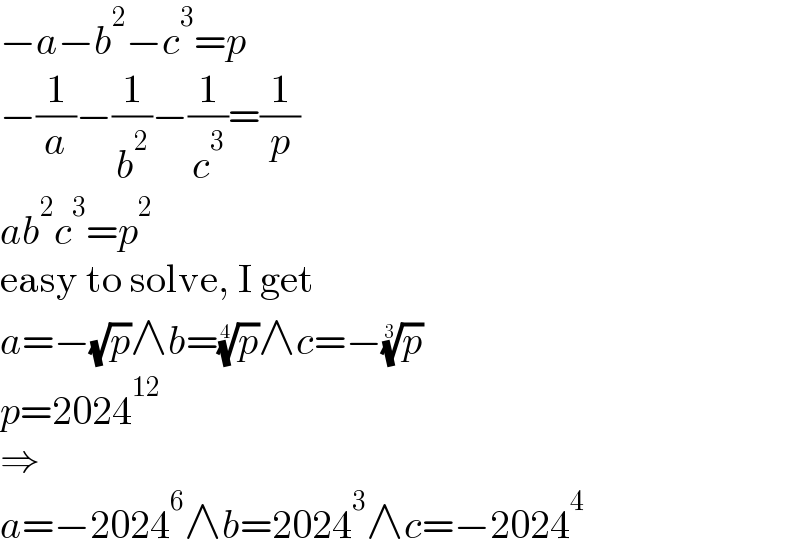
$$−{a}−{b}^{\mathrm{2}} −{c}^{\mathrm{3}} ={p} \\ $$$$−\frac{\mathrm{1}}{{a}}−\frac{\mathrm{1}}{{b}^{\mathrm{2}} }−\frac{\mathrm{1}}{{c}^{\mathrm{3}} }=\frac{\mathrm{1}}{{p}} \\ $$$${ab}^{\mathrm{2}} {c}^{\mathrm{3}} ={p}^{\mathrm{2}} \\ $$$$\mathrm{easy}\:\mathrm{to}\:\mathrm{solve},\:\mathrm{I}\:\mathrm{get} \\ $$$${a}=−\sqrt{{p}}\wedge{b}=\sqrt[{\mathrm{4}}]{{p}}\wedge{c}=−\sqrt[{\mathrm{3}}]{{p}} \\ $$$${p}=\mathrm{2024}^{\mathrm{12}} \\ $$$$\Rightarrow \\ $$$${a}=−\mathrm{2024}^{\mathrm{6}} \wedge{b}=\mathrm{2024}^{\mathrm{3}} \wedge{c}=−\mathrm{2024}^{\mathrm{4}} \\ $$
