
Question Number 138783 by mathdanisur last updated on 18/Apr/21
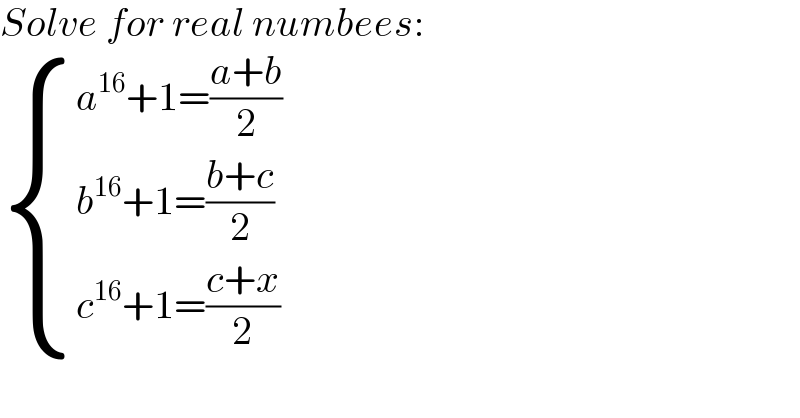
$${Solve}\:{for}\:{real}\:{numbees}: \\ $$$$\begin{cases}{{a}^{\mathrm{16}} +\mathrm{1}=\frac{{a}+{b}}{\mathrm{2}}}\\{{b}^{\mathrm{16}} +\mathrm{1}=\frac{{b}+{c}}{\mathrm{2}}}\\{{c}^{\mathrm{16}} +\mathrm{1}=\frac{{c}+{x}}{\mathrm{2}}}\end{cases} \\ $$
Commented by mr W last updated on 18/Apr/21

$${no}\:{real}\:{roots}! \\ $$
Commented by mathdanisur last updated on 18/Apr/21
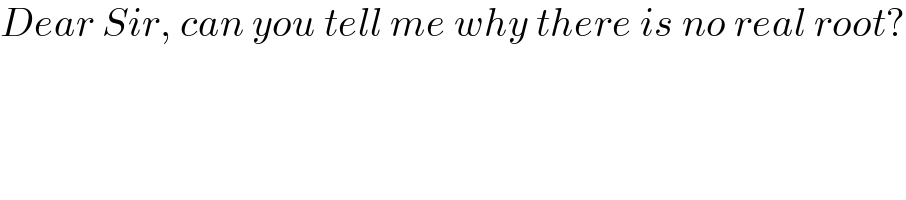
$${Dear}\:{Sir},\:{can}\:{you}\:{tell}\:{me}\:{why}\:{there}\:{is}\:{no}\:{real}\:{root}? \\ $$
Commented by mr W last updated on 18/Apr/21

$${if}\:{a}={t}\:{is}\:{a}\:{root},\:{then}\:{b}={t}\:{and}\:{c}={t}\:{are} \\ $$$${also}\:{roots}. \\ $$$${t}^{\mathrm{16}} +\mathrm{1}=\frac{{t}+{t}}{\mathrm{2}} \\ $$$${t}^{\mathrm{16}} −{t}+\mathrm{1}=\mathrm{0}\:? \\ $$$$ \\ $$$${f}\left({t}\right)={t}^{\mathrm{16}} −{t}+\mathrm{1} \\ $$$${f}'\left({t}\right)=\mathrm{16}{t}^{\mathrm{15}} −\mathrm{1}=\mathrm{0}\:\Rightarrow{t}=\frac{\mathrm{1}}{\:\sqrt[{\mathrm{15}}]{\mathrm{16}}} \\ $$$${f}''\left({t}\right)=\mathrm{16}×\mathrm{15}{t}^{\mathrm{14}} >\mathrm{0} \\ $$$${i}.{e}.\:{f}_{{min}} \:{is}\:{f}\left(\frac{\mathrm{1}}{\:\sqrt[{\mathrm{15}}]{\mathrm{16}}}\right)=\frac{\mathrm{1}}{\mathrm{16}^{\frac{\mathrm{16}}{\mathrm{15}}} }−\frac{\mathrm{1}}{\mathrm{16}^{\frac{\mathrm{1}}{\mathrm{15}}} }+\mathrm{1}\approx\mathrm{0}.\mathrm{2207} \\ $$$${since}\:{t}^{\mathrm{16}} −{t}+\mathrm{1}\geqslant\mathrm{0}.\mathrm{2207} \\ $$$${therefore}\:{t}^{\mathrm{16}} −{t}+\mathrm{1}=\mathrm{0}\:{has}\:{no}\:{real}\:{roots}. \\ $$
Commented by mathdanisur last updated on 18/Apr/21
$${Thank}\:{you}\:{very}\:{much}\:{dear}\:{Sir} \\ $$
