
Question Number 138764 by otchereabdullai@gmail.com last updated on 17/Apr/21

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{impedence}\:\mathrm{of}\:\mathrm{an}\:\mathrm{RC}\:\mathrm{circuit} \\ $$$$\mathrm{with}\:\mathrm{R}=\:\mathrm{10}\Omega\:\mathrm{and}\:\mathrm{C}=\mathrm{10}\mu\mathrm{F}\:\mathrm{at}\:\mathrm{an}\: \\ $$$$\mathrm{angular}\:\mathrm{frequency}\:\mathrm{of}\:\mathrm{21800rads}^{−\mathrm{1}} \\ $$
Answered by ajfour last updated on 18/Apr/21
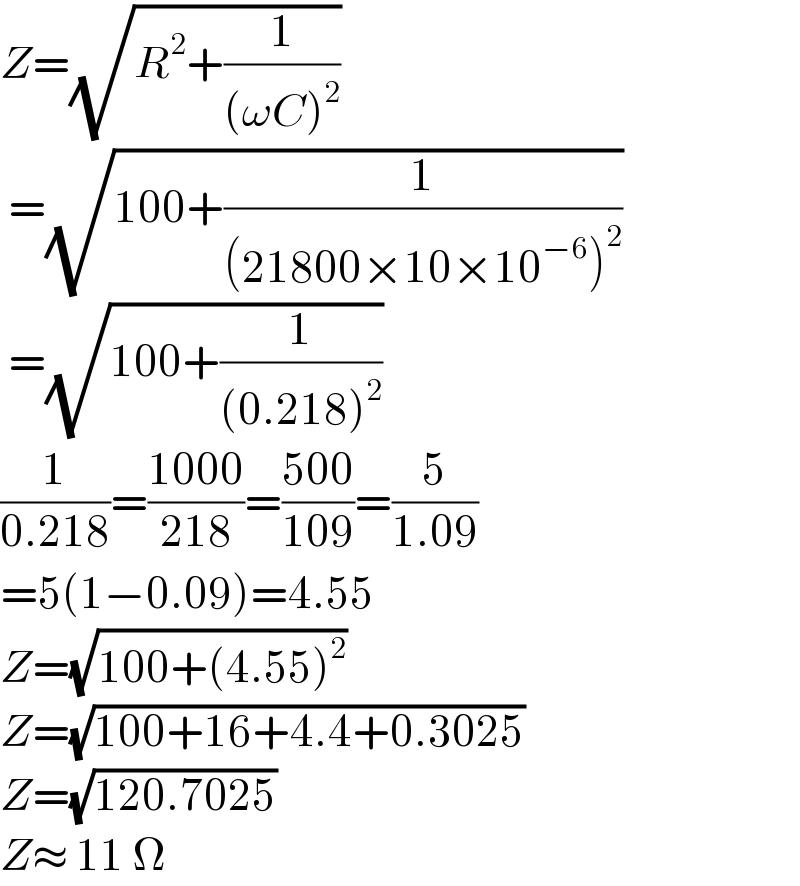
$${Z}=\sqrt{{R}^{\mathrm{2}} +\frac{\mathrm{1}}{\left(\omega{C}\right)^{\mathrm{2}} }} \\ $$$$\:=\sqrt{\mathrm{100}+\frac{\mathrm{1}}{\left(\mathrm{21800}×\mathrm{10}×\mathrm{10}^{−\mathrm{6}} \right)^{\mathrm{2}} }} \\ $$$$\:=\sqrt{\mathrm{100}+\frac{\mathrm{1}}{\left(\mathrm{0}.\mathrm{218}\right)^{\mathrm{2}} }} \\ $$$$\frac{\mathrm{1}}{\mathrm{0}.\mathrm{218}}=\frac{\mathrm{1000}}{\mathrm{218}}=\frac{\mathrm{500}}{\mathrm{109}}=\frac{\mathrm{5}}{\mathrm{1}.\mathrm{09}} \\ $$$$=\mathrm{5}\left(\mathrm{1}−\mathrm{0}.\mathrm{09}\right)=\mathrm{4}.\mathrm{55} \\ $$$${Z}=\sqrt{\mathrm{100}+\left(\mathrm{4}.\mathrm{55}\right)^{\mathrm{2}} } \\ $$$${Z}=\sqrt{\mathrm{100}+\mathrm{16}+\mathrm{4}.\mathrm{4}+\mathrm{0}.\mathrm{3025}} \\ $$$${Z}=\sqrt{\mathrm{120}.\mathrm{7025}} \\ $$$${Z}\approx\:\mathrm{11}\:\Omega \\ $$
Commented by otchereabdullai@gmail.com last updated on 18/Apr/21

$$\mathrm{Thanks}\:\mathrm{a}\:\mathrm{lot}\:\mathrm{prof}\:\mathrm{ajour} \\ $$
Answered by physicstutes last updated on 18/Apr/21
![impedance Z =(√(R^2 +(X_L −X_C )^2 )) but X_L = 0 since we have an R−C circuit. ⇒ Z = (√(R^2 +X_C ^2 )) where X_C = (1/(2πfC)) = (1/(ωC)) = (1/((21800)(10×10^(−6) ))) ⇒ Z = (√(10^2 +[(1/((21800)(10×10^(−6) )))]^2 )) ≈ 11 Ω](Q138805.png)
$$\mathrm{impedance}\:\mathrm{Z}\:=\sqrt{{R}^{\mathrm{2}} +\left({X}_{{L}} −{X}_{{C}} \right)^{\mathrm{2}} } \\ $$$$\mathrm{but}\:{X}_{{L}} \:=\:\mathrm{0}\:\mathrm{since}\:\mathrm{we}\:\mathrm{have}\:\mathrm{an}\:\mathrm{R}−\mathrm{C}\:\mathrm{circuit}. \\ $$$$\Rightarrow\:{Z}\:=\:\sqrt{{R}^{\mathrm{2}} +{X}_{{C}} ^{\mathrm{2}} } \\ $$$$\mathrm{where}\:{X}_{{C}} \:=\:\frac{\mathrm{1}}{\mathrm{2}\pi{fC}}\:=\:\frac{\mathrm{1}}{\omega{C}}\:=\:\frac{\mathrm{1}}{\left(\mathrm{21800}\right)\left(\mathrm{10}×\mathrm{10}^{−\mathrm{6}} \right)} \\ $$$$\Rightarrow\:{Z}\:=\:\sqrt{\mathrm{10}^{\mathrm{2}} +\left[\frac{\mathrm{1}}{\left(\mathrm{21800}\right)\left(\mathrm{10}×\mathrm{10}^{−\mathrm{6}} \right)}\right]^{\mathrm{2}} }\:\approx\:\mathrm{11}\:\Omega \\ $$
Commented by otchereabdullai@gmail.com last updated on 18/Apr/21

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\:\mathrm{physicstutes} \\ $$
