
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 138748 by physicstutes last updated on 17/Apr/21

$$\mathrm{A}\:\mathrm{committee}\:\mathrm{of}\:\mathrm{3}\:\mathrm{members}\:\mathrm{is}\:\mathrm{to}\:\mathrm{be}\:\mathrm{formed}\:\mathrm{from}\:\mathrm{8}\:\mathrm{members}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{committees}\:\mathrm{that}\:\mathrm{can}\:\mathrm{be}\:\mathrm{formed}\:\mathrm{if}\:\mathrm{two}\:\mathrm{particular} \\ $$$$\mathrm{club}\:\mathrm{members}\:\mathrm{cannot}\:\mathrm{both}\:\mathrm{be}\:\mathrm{in}\:\mathrm{a}\:\mathrm{committee} \\ $$
Answered by mr W last updated on 17/Apr/21

$${C}_{\mathrm{3}} ^{\mathrm{8}} −{C}_{\mathrm{1}} ^{\mathrm{6}} =\mathrm{50} \\ $$
Commented by physicstutes last updated on 17/Apr/21
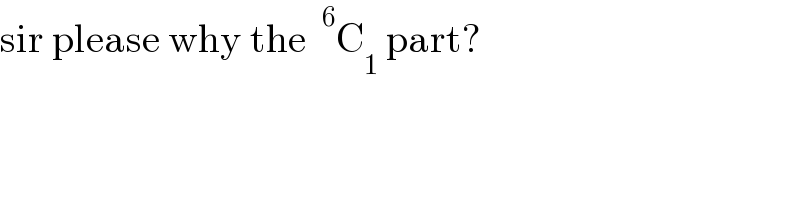
$$\mathrm{sir}\:\mathrm{please}\:\mathrm{why}\:\mathrm{the}\:\:^{\mathrm{6}} \mathrm{C}_{\mathrm{1}} \:\mathrm{part}? \\ $$
Commented by mr W last updated on 17/Apr/21

$${to}\:{select}\:\mathrm{3}\:{from}\:\mathrm{8}\:{persons}\:{there}\:{are} \\ $$$${totally}\:{C}_{\mathrm{3}} ^{\mathrm{8}} \:{ways}. \\ $$$${if}\:{two}\:{particular}\:{persons}\:{are}\:{in}\:{the} \\ $$$${committee},\:{to}\:{select}\:{the}\:{third}\:{person} \\ $$$${from}\:{the}\:{rest}\:\mathrm{6}\:{persons},\:{there}\:{are} \\ $$$${C}_{\mathrm{1}} ^{\mathrm{6}} \:{ways}. \\ $$$${since}\:{these}\:{two}\:{particular}\:{persons} \\ $$$${should}\:{not}\:{be}\:{both}\:{in}\:{the}\:{committee}, \\ $$$${so}\:{we}\:{have}\:{only}\:{C}_{\mathrm{3}} ^{\mathrm{8}} −{C}_{\mathrm{1}} ^{\mathrm{6}} \:{ways}. \\ $$
Commented by mr W last updated on 17/Apr/21
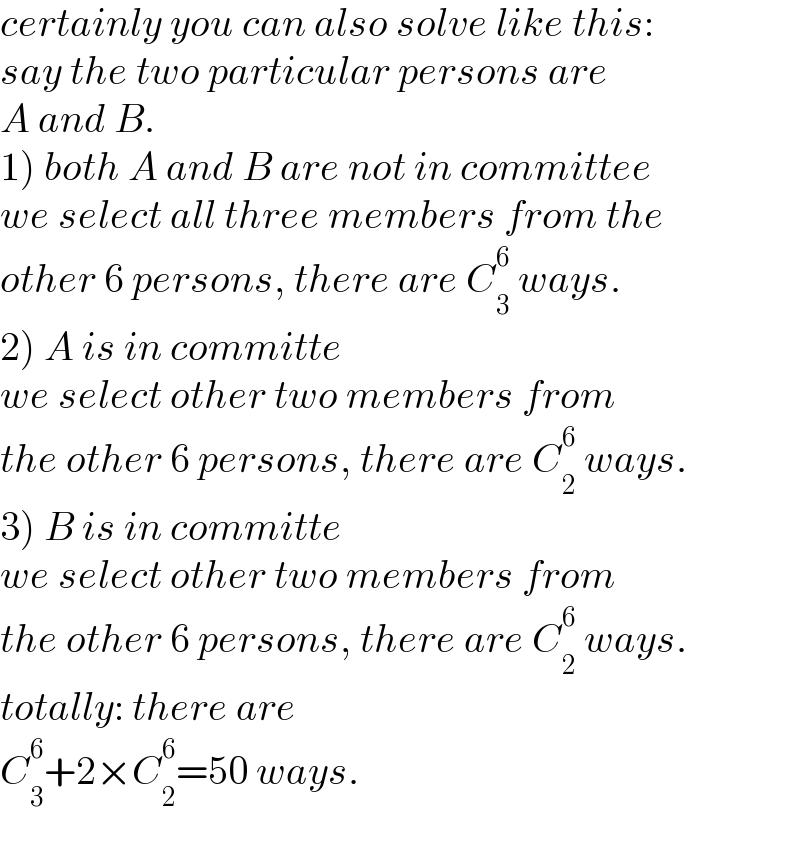
$${certainly}\:{you}\:{can}\:{also}\:{solve}\:{like}\:{this}: \\ $$$${say}\:{the}\:{two}\:{particular}\:{persons}\:{are} \\ $$$${A}\:{and}\:{B}. \\ $$$$\left.\mathrm{1}\right)\:{both}\:{A}\:{and}\:{B}\:{are}\:{not}\:{in}\:{committee} \\ $$$${we}\:{select}\:{all}\:{three}\:{members}\:{from}\:{the} \\ $$$${other}\:\mathrm{6}\:{persons},\:{there}\:{are}\:{C}_{\mathrm{3}} ^{\mathrm{6}} \:{ways}. \\ $$$$\left.\mathrm{2}\right)\:{A}\:{is}\:{in}\:{committe} \\ $$$${we}\:{select}\:{other}\:{two}\:{members}\:{from} \\ $$$${the}\:{other}\:\mathrm{6}\:{persons},\:{there}\:{are}\:{C}_{\mathrm{2}} ^{\mathrm{6}} \:{ways}. \\ $$$$\left.\mathrm{3}\right)\:{B}\:{is}\:{in}\:{committe} \\ $$$${we}\:{select}\:{other}\:{two}\:{members}\:{from} \\ $$$${the}\:{other}\:\mathrm{6}\:{persons},\:{there}\:{are}\:{C}_{\mathrm{2}} ^{\mathrm{6}} \:{ways}. \\ $$$${totally}:\:{there}\:{are} \\ $$$${C}_{\mathrm{3}} ^{\mathrm{6}} +\mathrm{2}×{C}_{\mathrm{2}} ^{\mathrm{6}} =\mathrm{50}\:{ways}. \\ $$
Commented by physicstutes last updated on 18/Apr/21
$$\mathrm{that}\:\mathrm{was}\:\mathrm{brilliant}\:\mathrm{sir}.\:\mathrm{Thanks} \\ $$
