
Question Number 92179 by otchereabdullai@gmail.com last updated on 05/May/20
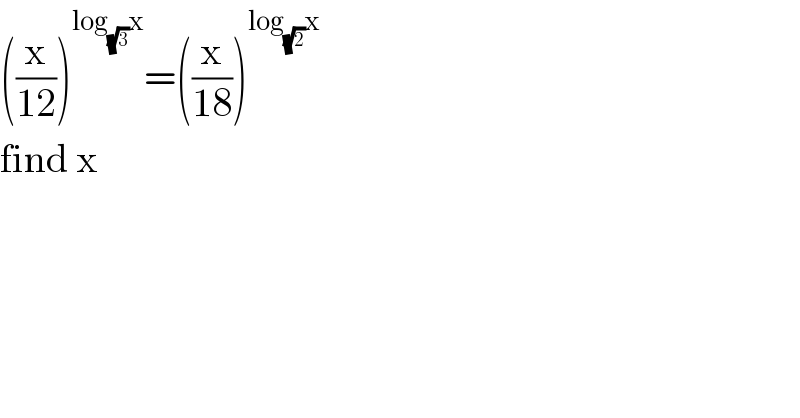
$$\left(\frac{\mathrm{x}}{\mathrm{12}}\right)^{\mathrm{log}_{\sqrt{\mathrm{3}}} \mathrm{x}} =\left(\frac{\mathrm{x}}{\mathrm{18}}\right)^{\mathrm{log}_{\sqrt{\mathrm{2}}} \mathrm{x}} \\ $$$$\mathrm{find}\:\mathrm{x} \\ $$
Commented by john santu last updated on 05/May/20
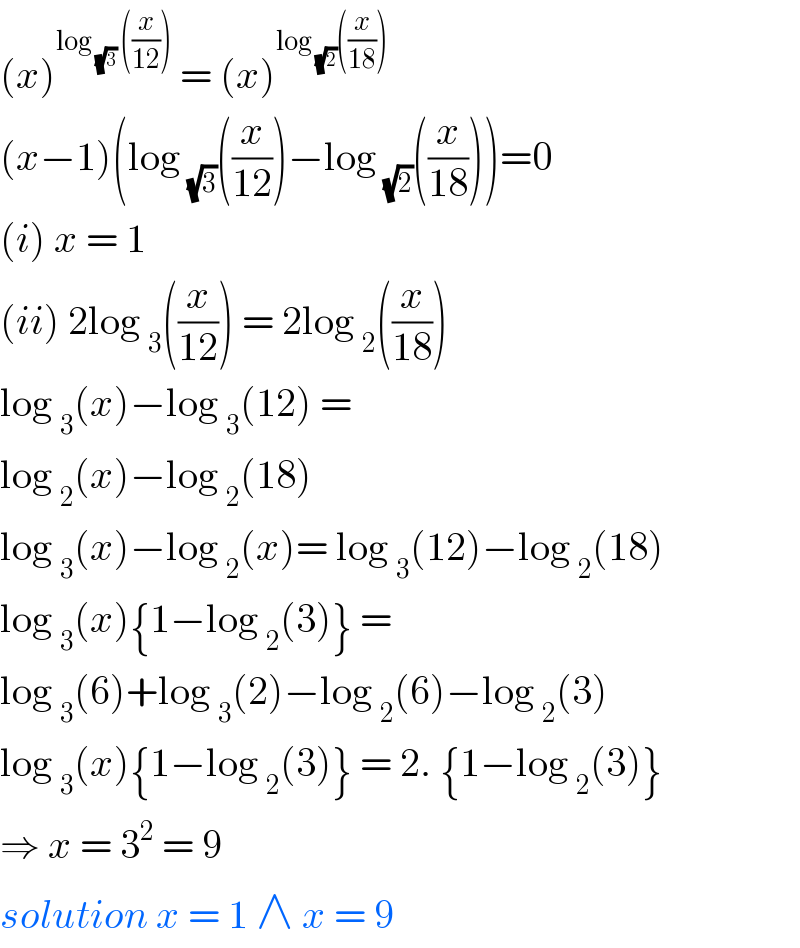
$$\left({x}\right)^{\mathrm{log}\:_{\sqrt{\mathrm{3}}} \:\left(\frac{{x}}{\mathrm{12}}\right)} \:=\:\left({x}\right)^{\mathrm{log}\:_{\sqrt{\mathrm{2}}} \left(\frac{{x}}{\mathrm{18}}\right)} \\ $$$$\left({x}−\mathrm{1}\right)\left(\mathrm{log}\:_{\sqrt{\mathrm{3}}} \left(\frac{{x}}{\mathrm{12}}\right)−\mathrm{log}\:_{\sqrt{\mathrm{2}}} \left(\frac{{x}}{\mathrm{18}}\right)\right)=\mathrm{0} \\ $$$$\left({i}\right)\:{x}\:=\:\mathrm{1} \\ $$$$\left({ii}\right)\:\mathrm{2log}\:_{\mathrm{3}} \left(\frac{{x}}{\mathrm{12}}\right)\:=\:\mathrm{2log}\:_{\mathrm{2}} \left(\frac{{x}}{\mathrm{18}}\right) \\ $$$$\mathrm{log}\:_{\mathrm{3}} \left({x}\right)−\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{12}\right)\:=\: \\ $$$$\mathrm{log}\:_{\mathrm{2}} \left({x}\right)−\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{18}\right)\: \\ $$$$\mathrm{log}\:_{\mathrm{3}} \left({x}\right)−\mathrm{log}\:_{\mathrm{2}} \left({x}\right)=\:\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{12}\right)−\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{18}\right) \\ $$$$\mathrm{log}\:_{\mathrm{3}} \left({x}\right)\left\{\mathrm{1}−\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{3}\right)\right\}\:= \\ $$$$\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{6}\right)+\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{2}\right)−\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{6}\right)−\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{3}\right) \\ $$$$\mathrm{log}\:_{\mathrm{3}} \left({x}\right)\left\{\mathrm{1}−\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{3}\right)\right\}\:=\:\mathrm{2}.\:\left\{\mathrm{1}−\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{3}\right)\right\} \\ $$$$\Rightarrow\:{x}\:=\:\mathrm{3}^{\mathrm{2}} \:=\:\mathrm{9}\: \\ $$$${solution}\:{x}\:=\:\mathrm{1}\:\wedge\:{x}\:=\:\mathrm{9} \\ $$
Commented by jagoll last updated on 05/May/20
good ☺☺☺✔️
Commented by otchereabdullai@gmail.com last updated on 05/May/20
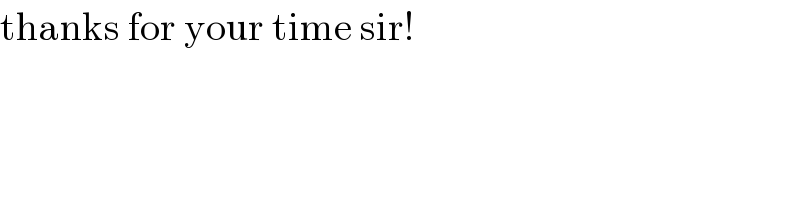
$$\mathrm{thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}! \\ $$
Commented by otchereabdullai@gmail.com last updated on 05/May/20

$$\mathrm{but}\:\mathrm{sir}\:\mathrm{pls}\:\:\mathrm{x}=\:\mathrm{9}\:\mathrm{do}\:\mathrm{not}\:\mathrm{satisfy}\: \\ $$
Commented by otchereabdullai@gmail.com last updated on 05/May/20

$$\mathrm{and}\:\mathrm{please}\:\mathrm{the}\:\mathrm{base}\:\mathrm{in}\:\mathrm{the}\:\mathrm{question}\: \\ $$$$\mathrm{was}\:\:\sqrt{\mathrm{3}}\:\:\mathrm{and}\:\sqrt{\mathrm{2}\:}\:\:\:\mathrm{in}\:\left(\mathrm{ii}\right)\:\mathrm{but}\:\mathrm{pls}\:\mathrm{why}\:\mathrm{base}\:\mathrm{3}\:\mathrm{and} \\ $$$$\mathrm{2}\:\:\mathrm{please}\:\mathrm{i}\:\mathrm{want}\:\mathrm{to}\:\mathrm{understand}\:\mathrm{thanks}\: \\ $$$$\mathrm{sir} \\ $$
Commented by otchereabdullai@gmail.com last updated on 05/May/20

$$\mathrm{am}\:\mathrm{much}\:\mathrm{greatful}\:\mathrm{sir}\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}! \\ $$
Commented by john santu last updated on 05/May/20

$$\left(\mathrm{9}\right)^{\mathrm{log}\:_{\sqrt{\mathrm{3}}} \left(\frac{\mathrm{9}}{\mathrm{12}}\right)} \:=\:\left(\mathrm{9}\right)^{\mathrm{log}\:_{\mathrm{3}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} } \\ $$$$\left(\mathrm{3}\right)^{\mathrm{log}\:_{\mathrm{3}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{4}} } \:=\:\frac{\mathrm{81}}{\mathrm{256}}\:\left(\mathrm{Lhs}\right) \\ $$$$\mathrm{Rhs}\:\left(\mathrm{9}\right)^{\mathrm{log}\:_{\sqrt{\mathrm{2}}} \left(\frac{\mathrm{9}}{\mathrm{18}}\right)} \:=\:\left(\mathrm{9}\right)^{\mathrm{log}\:_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)} \\ $$$$=\left(\mathrm{3}\right)^{\mathrm{log}\:_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{16}}\right)} \:=\:\frac{\mathrm{1}}{\mathrm{81}} \\ $$$$\mathrm{Lhs}\:\neq\:\mathrm{Rhs}\: \\ $$$$\mathrm{x}\:=\:\mathrm{1}\:\mathrm{only}\:\mathrm{solution}\: \\ $$$$ \\ $$
Commented by john santu last updated on 05/May/20

$$\mathrm{we}\:\mathrm{know}\:\mathrm{property}\:\mathrm{of}\:\mathrm{logarithm} \\ $$$$\mathrm{a}^{\mathrm{log}\:_{\mathrm{b}} \left(\mathrm{c}\right)} \:=\:\mathrm{c}^{\mathrm{log}\:_{\mathrm{b}} \left(\mathrm{a}\right)} \: \\ $$
Commented by john santu last updated on 05/May/20
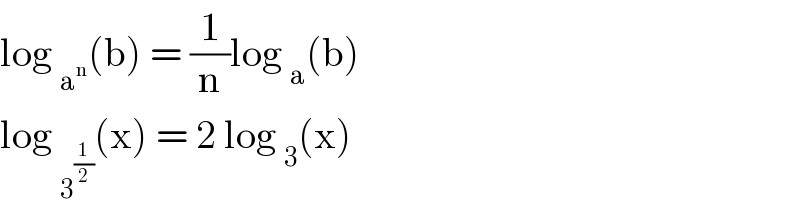
$$\mathrm{log}\:_{\mathrm{a}^{\mathrm{n}} } \left(\mathrm{b}\right)\:=\:\frac{\mathrm{1}}{\mathrm{n}}\mathrm{log}\:_{\mathrm{a}} \left(\mathrm{b}\right)\: \\ $$$$\mathrm{log}\:_{\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{2}}} } \left(\mathrm{x}\right)\:=\:\mathrm{2}\:\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{x}\right) \\ $$
Commented by otchereabdullai@gmail.com last updated on 05/May/20
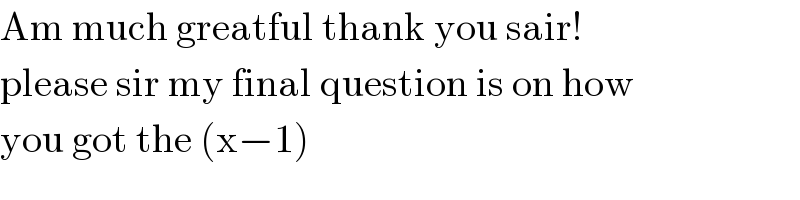
$$\mathrm{Am}\:\mathrm{much}\:\mathrm{greatful}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{sair}! \\ $$$$\mathrm{please}\:\mathrm{sir}\:\mathrm{my}\:\mathrm{final}\:\mathrm{question}\:\mathrm{is}\:\mathrm{on}\:\mathrm{how} \\ $$$$\mathrm{you}\:\mathrm{got}\:\mathrm{the}\:\left(\mathrm{x}−\mathrm{1}\right) \\ $$
Commented by jagoll last updated on 05/May/20
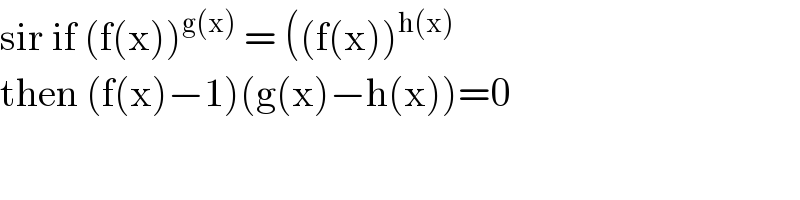
$$\mathrm{sir}\:\mathrm{if}\:\left(\mathrm{f}\left(\mathrm{x}\right)\right)^{\mathrm{g}\left(\mathrm{x}\right)} \:=\:\left(\left(\mathrm{f}\left(\mathrm{x}\right)\right)^{\mathrm{h}\left(\mathrm{x}\right)} \:\right. \\ $$$$\mathrm{then}\:\left(\mathrm{f}\left(\mathrm{x}\right)−\mathrm{1}\right)\left(\mathrm{g}\left(\mathrm{x}\right)−\mathrm{h}\left(\mathrm{x}\right)\right)=\mathrm{0}\: \\ $$
Commented by otchereabdullai@gmail.com last updated on 05/May/20

$$\mathrm{a}\:\mathrm{have}\:\mathrm{really}\:\mathrm{enjoy}\:\mathrm{your}\:\mathrm{lesson} \\ $$$$\mathrm{God}\:\mathrm{richly}\:\mathrm{bless}\:\mathrm{you} \\ $$
