
Question Number 138661 by mr W last updated on 16/Apr/21
Commented by mr W last updated on 16/Apr/21

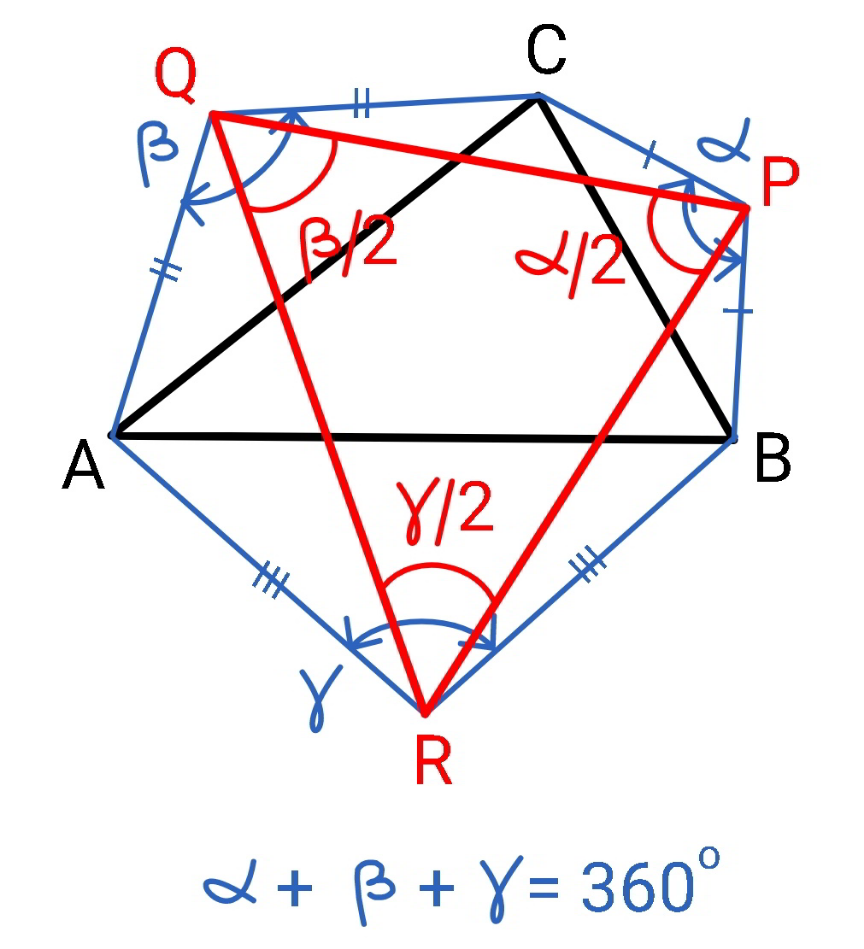
$${proof}\:{for}\:{Q}\mathrm{138519} \\ $$
Commented by mr W last updated on 16/Apr/21
Commented by mr W last updated on 16/Apr/21

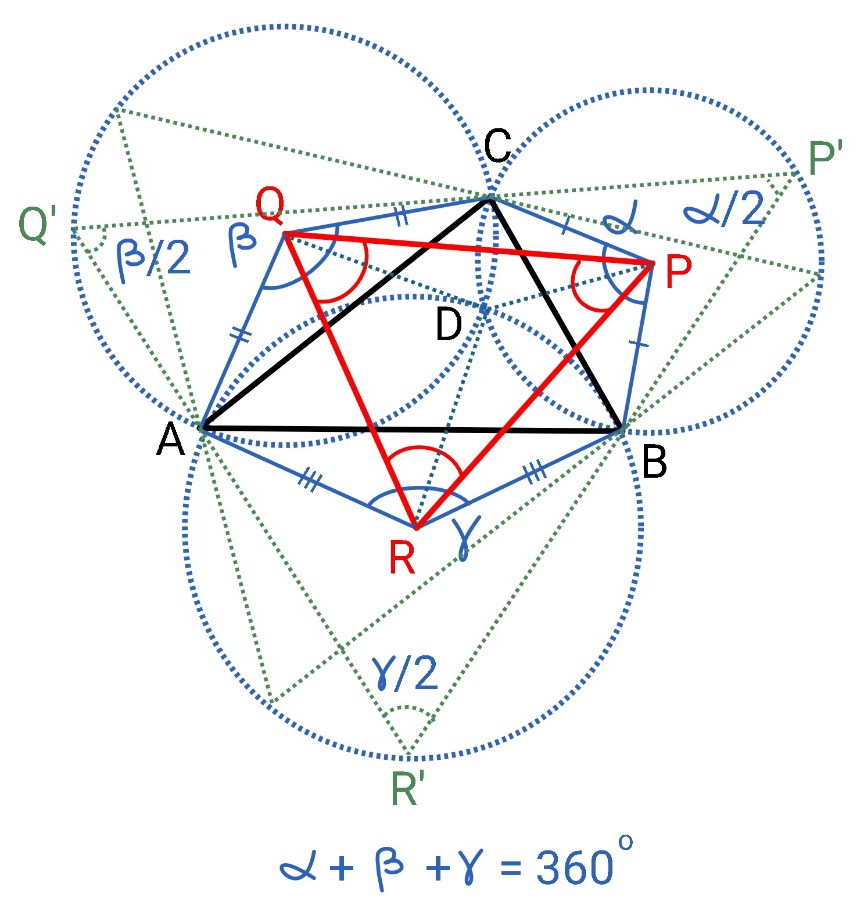
$$\alpha+\beta+\gamma=\mathrm{360}° \\ $$$$\Rightarrow\frac{\alpha}{\mathrm{2}}+\frac{\beta}{\mathrm{2}}+\frac{\gamma}{\mathrm{2}}=\mathrm{180}° \\ $$$${that}\:{means}\:{triangles}\:{with}\:{interior} \\ $$$${angles}\:\frac{\alpha}{\mathrm{2}},\frac{\beta}{\mathrm{2}},\frac{\gamma}{\mathrm{2}}\:{can}\:{be}\:{formed},\:{such} \\ $$$${as}\:\Delta{P}'{Q}'{R}',\:{see}\:{diagram}\:{above}. \\ $$$${the}\:{circles}\:{with}\:{centers}\:{at}\:{P},{Q},{R}\: \\ $$$${intersect}\:{at}\:{point}\:{D}. \\ $$$$\angle{DPQ}=\frac{\angle{DPC}}{\mathrm{2}} \\ $$$$\angle{DPR}=\frac{\angle{DPB}}{\mathrm{2}} \\ $$$$\angle{P}=\angle{DPQ}+\angle{DPR}=\frac{\angle{DPC}+\angle{DPB}}{\mathrm{2}}=\frac{\alpha}{\mathrm{2}} \\ $$$${similarly} \\ $$$$\angle{Q}=\frac{\beta}{\mathrm{2}} \\ $$$$\angle{R}=\frac{\gamma}{\mathrm{2}} \\ $$
