
Question Number 138612 by SOMEDAVONG last updated on 15/Apr/21
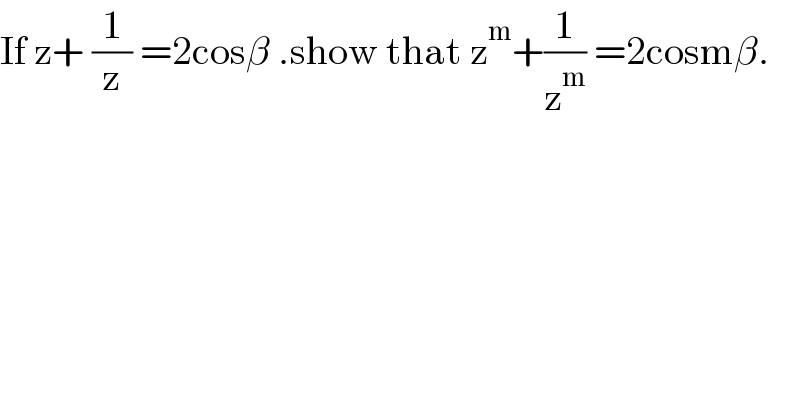
$$\mathrm{If}\:\mathrm{z}+\:\frac{\mathrm{1}}{\mathrm{z}}\:=\mathrm{2cos}\beta\:.\mathrm{show}\:\mathrm{that}\:\mathrm{z}^{\mathrm{m}} +\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{m}} }\:=\mathrm{2cosm}\beta. \\ $$
Answered by Ar Brandon last updated on 15/Apr/21
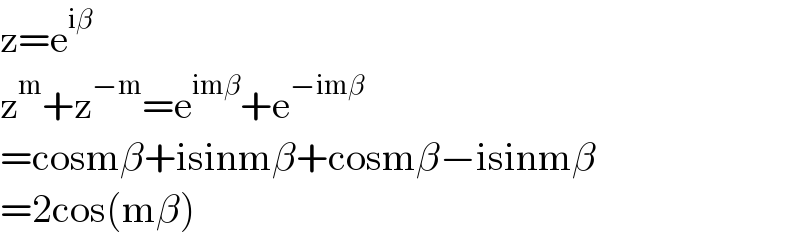
$$\mathrm{z}=\mathrm{e}^{\mathrm{i}\beta} \\ $$$$\mathrm{z}^{\mathrm{m}} +\mathrm{z}^{−\mathrm{m}} =\mathrm{e}^{\mathrm{im}\beta} +\mathrm{e}^{−\mathrm{im}\beta} \\ $$$$=\mathrm{cosm}\beta+\mathrm{isinm}\beta+\mathrm{cosm}\beta−\mathrm{isinm}\beta \\ $$$$=\mathrm{2cos}\left(\mathrm{m}\beta\right) \\ $$
