
Question Number 138571 by bemath last updated on 15/Apr/21
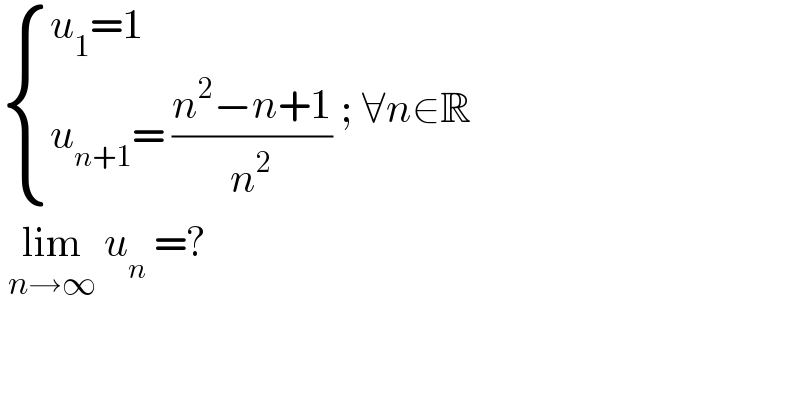
$$\begin{cases}{{u}_{\mathrm{1}} =\mathrm{1}}\\{{u}_{{n}+\mathrm{1}} =\:\frac{{n}^{\mathrm{2}} −{n}+\mathrm{1}}{{n}^{\mathrm{2}} }}\end{cases}\:;\:\forall{n}\in\mathbb{R} \\ $$$$\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{u}_{{n}} \:=? \\ $$
Answered by mathmax by abdo last updated on 15/Apr/21
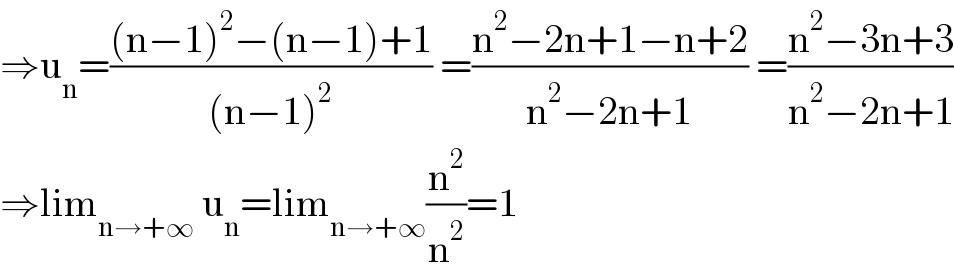
$$\Rightarrow\mathrm{u}_{\mathrm{n}} =\frac{\left(\mathrm{n}−\mathrm{1}\right)^{\mathrm{2}} −\left(\mathrm{n}−\mathrm{1}\right)+\mathrm{1}}{\left(\mathrm{n}−\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{n}^{\mathrm{2}} −\mathrm{2n}+\mathrm{1}−\mathrm{n}+\mathrm{2}}{\mathrm{n}^{\mathrm{2}} −\mathrm{2n}+\mathrm{1}}\:=\frac{\mathrm{n}^{\mathrm{2}} −\mathrm{3n}+\mathrm{3}}{\mathrm{n}^{\mathrm{2}} −\mathrm{2n}+\mathrm{1}} \\ $$$$\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{u}_{\mathrm{n}} =\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }=\mathrm{1} \\ $$
