
Question Number 138560 by Raxreedoroid last updated on 14/Apr/21
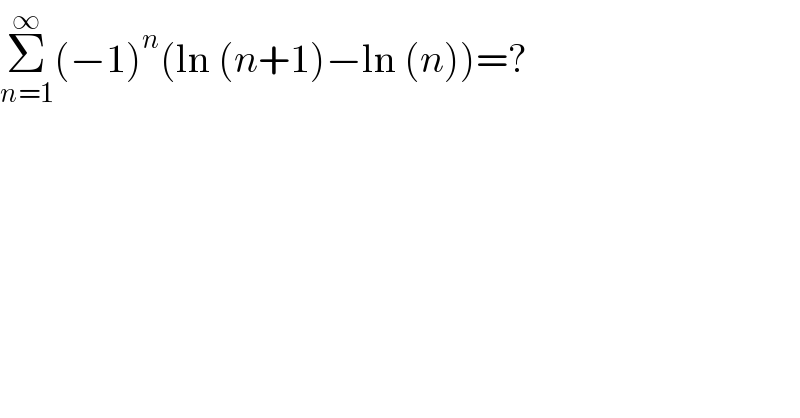
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \left(\mathrm{ln}\:\left({n}+\mathrm{1}\right)−\mathrm{ln}\:\left({n}\right)\right)=? \\ $$
Answered by Dwaipayan Shikari last updated on 14/Apr/21
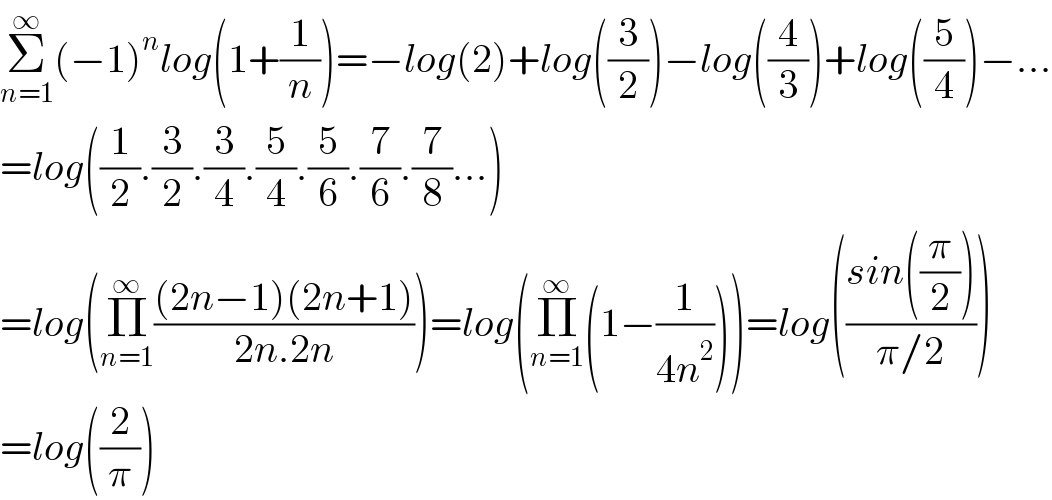
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} {log}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)=−{log}\left(\mathrm{2}\right)+{log}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−{log}\left(\frac{\mathrm{4}}{\mathrm{3}}\right)+{log}\left(\frac{\mathrm{5}}{\mathrm{4}}\right)−... \\ $$$$={log}\left(\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{3}}{\mathrm{2}}.\frac{\mathrm{3}}{\mathrm{4}}.\frac{\mathrm{5}}{\mathrm{4}}.\frac{\mathrm{5}}{\mathrm{6}}.\frac{\mathrm{7}}{\mathrm{6}}.\frac{\mathrm{7}}{\mathrm{8}}...\right) \\ $$$$={log}\left(\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\frac{\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{2}{n}.\mathrm{2}{n}}\right)={log}\left(\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} }\right)\right)={log}\left(\frac{{sin}\left(\frac{\pi}{\mathrm{2}}\right)}{\pi/\mathrm{2}}\right) \\ $$$$={log}\left(\frac{\mathrm{2}}{\pi}\right) \\ $$
