
Question Number 138424 by tugu last updated on 13/Apr/21
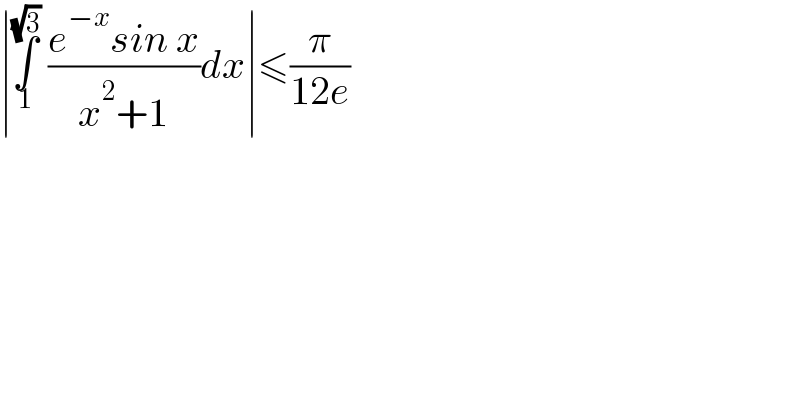
$$\mid\underset{\mathrm{1}} {\overset{\sqrt{\mathrm{3}}} {\int}}\:\frac{{e}^{−{x}} {sin}\:{x}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}\mid\leqslant\frac{\pi}{\mathrm{12}{e}} \\ $$
Commented by mitica last updated on 14/Apr/21
![∃c∈[1,(√3)],∫_1 ^(√3) ((e^(−x) sinx)/(x^2 +1))dx=((sinc)/e^c ) ∫_1 ^(√3) (1/(x^2 +1))dx ∣((sinc)/e^c ) ∫_1 ^(√3) (1/(x^2 +1))dx∣≤(1/e^c )∙∣arctgx∣_1 ^(√3) ∣≤(1/e)((π/3)−(π/4))=(π/(12e))](Q138547.png)
$$\exists{c}\in\left[\mathrm{1},\sqrt{\mathrm{3}}\right],\underset{\mathrm{1}} {\overset{\sqrt{\mathrm{3}}} {\int}}\frac{{e}^{−{x}} {sinx}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}=\frac{{sinc}}{{e}^{{c}} }\:\underset{\mathrm{1}} {\overset{\sqrt{\mathrm{3}}} {\int}}\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$\mid\frac{{sinc}}{{e}^{{c}} }\:\underset{\mathrm{1}} {\overset{\sqrt{\mathrm{3}}} {\int}}\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}\mid\leqslant\frac{\mathrm{1}}{{e}^{{c}} }\centerdot\mid{arctgx}\mid_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} \mid\leqslant\frac{\mathrm{1}}{{e}}\left(\frac{\pi}{\mathrm{3}}−\frac{\pi}{\mathrm{4}}\right)=\frac{\pi}{\mathrm{12}{e}} \\ $$
