
Question Number 13840 by Tinkutara last updated on 24/May/17
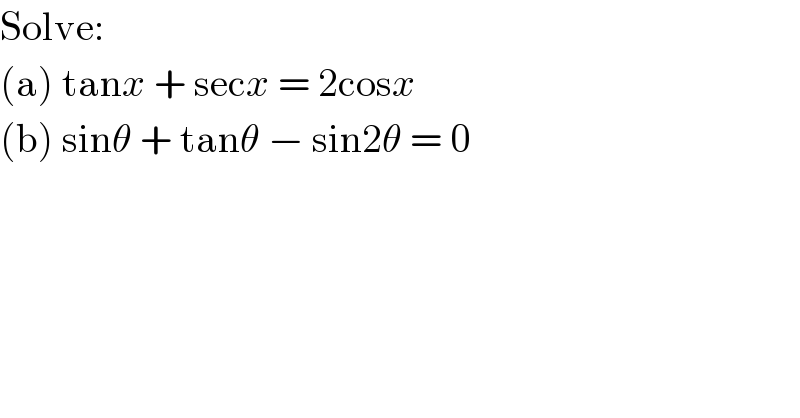
$$\mathrm{Solve}: \\ $$$$\left(\mathrm{a}\right)\:\mathrm{tan}{x}\:+\:\mathrm{sec}{x}\:=\:\mathrm{2cos}{x} \\ $$$$\left(\mathrm{b}\right)\:\mathrm{sin}\theta\:+\:\mathrm{tan}\theta\:−\:\mathrm{sin2}\theta\:=\:\mathrm{0} \\ $$
Answered by ajfour last updated on 24/May/17
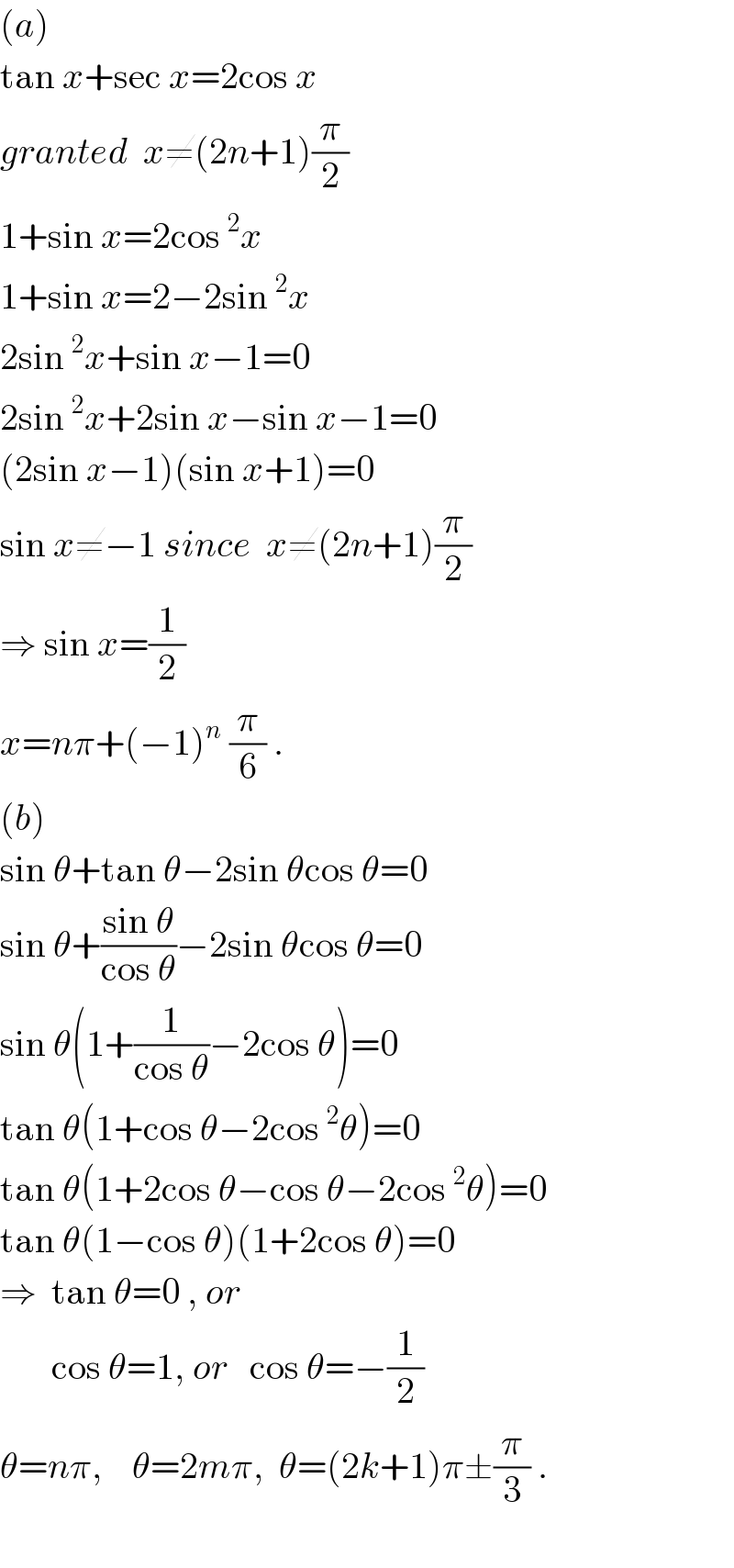
$$\left({a}\right) \\ $$$$\mathrm{tan}\:{x}+\mathrm{sec}\:{x}=\mathrm{2cos}\:{x} \\ $$$${granted}\:\:{x}\neq\left(\mathrm{2}{n}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{1}+\mathrm{sin}\:{x}=\mathrm{2cos}\:^{\mathrm{2}} {x} \\ $$$$\mathrm{1}+\mathrm{sin}\:{x}=\mathrm{2}−\mathrm{2sin}\:^{\mathrm{2}} {x} \\ $$$$\mathrm{2sin}\:^{\mathrm{2}} {x}+\mathrm{sin}\:{x}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{2sin}\:^{\mathrm{2}} {x}+\mathrm{2sin}\:{x}−\mathrm{sin}\:{x}−\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{2sin}\:{x}−\mathrm{1}\right)\left(\mathrm{sin}\:{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{sin}\:{x}\neq−\mathrm{1}\:{since}\:\:{x}\neq\left(\mathrm{2}{n}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{sin}\:{x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${x}={n}\pi+\left(−\mathrm{1}\right)^{{n}} \:\frac{\pi}{\mathrm{6}}\:. \\ $$$$\left({b}\right) \\ $$$$\mathrm{sin}\:\theta+\mathrm{tan}\:\theta−\mathrm{2sin}\:\theta\mathrm{cos}\:\theta=\mathrm{0} \\ $$$$\mathrm{sin}\:\theta+\frac{\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta}−\mathrm{2sin}\:\theta\mathrm{cos}\:\theta=\mathrm{0} \\ $$$$\mathrm{sin}\:\theta\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{cos}\:\theta}−\mathrm{2cos}\:\theta\right)=\mathrm{0} \\ $$$$\mathrm{tan}\:\theta\left(\mathrm{1}+\mathrm{cos}\:\theta−\mathrm{2cos}\:^{\mathrm{2}} \theta\right)=\mathrm{0} \\ $$$$\mathrm{tan}\:\theta\left(\mathrm{1}+\mathrm{2cos}\:\theta−\mathrm{cos}\:\theta−\mathrm{2cos}\:^{\mathrm{2}} \theta\right)=\mathrm{0} \\ $$$$\mathrm{tan}\:\theta\left(\mathrm{1}−\mathrm{cos}\:\theta\right)\left(\mathrm{1}+\mathrm{2cos}\:\theta\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{tan}\:\theta=\mathrm{0}\:,\:{or} \\ $$$$\:\:\:\:\:\:\:\mathrm{cos}\:\theta=\mathrm{1},\:{or}\:\:\:\mathrm{cos}\:\theta=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\theta={n}\pi,\:\:\:\:\theta=\mathrm{2}{m}\pi,\:\:\theta=\left(\mathrm{2}{k}+\mathrm{1}\right)\pi\pm\frac{\pi}{\mathrm{3}}\:. \\ $$$$ \\ $$
Commented by Tinkutara last updated on 24/May/17

$$\left(\mathrm{a}\right)\:\mathrm{part}\:\mathrm{is}\:\mathrm{wrong}\:\mathrm{because}\:\mathrm{you}\:\mathrm{noted} \\ $$$$\mathrm{down}\:\mathrm{the}\:\mathrm{incorrect}\:\mathrm{question};\:\mathrm{it}\:\mathrm{should} \\ $$$$\mathrm{be}\:\mathrm{2}\:\mathrm{cos}\:{x}\:\mathrm{instead}\:\mathrm{of}\:\mathrm{cos}\:{x}\:\mathrm{in}\:\mathrm{the}\:\mathrm{first} \\ $$$$\mathrm{line}. \\ $$
Commented by Tinkutara last updated on 24/May/17
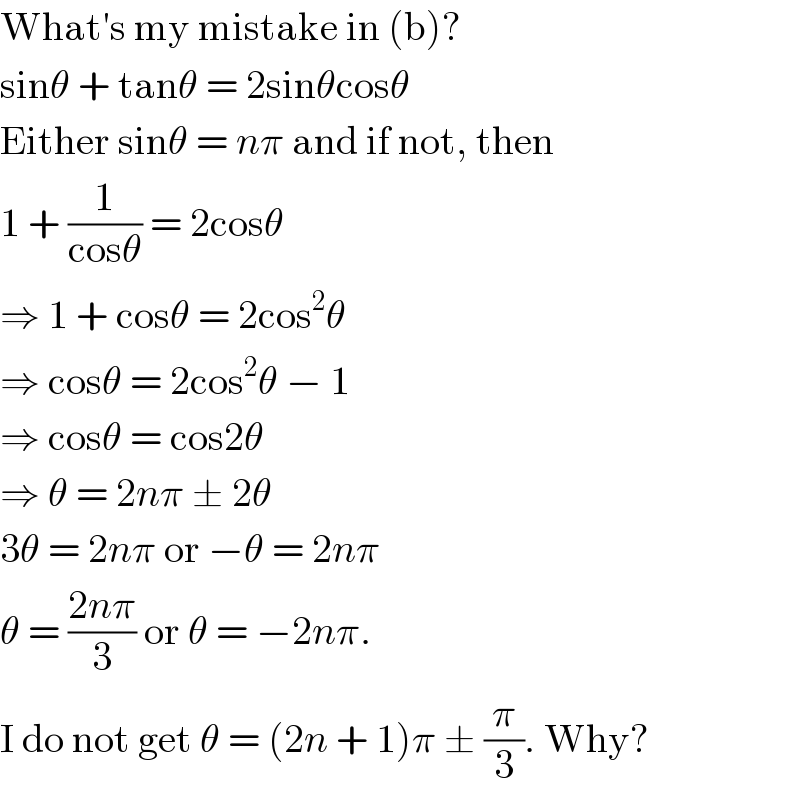
$$\mathrm{What}'\mathrm{s}\:\mathrm{my}\:\mathrm{mistake}\:\mathrm{in}\:\left(\mathrm{b}\right)? \\ $$$$\mathrm{sin}\theta\:+\:\mathrm{tan}\theta\:=\:\mathrm{2sin}\theta\mathrm{cos}\theta \\ $$$$\mathrm{Either}\:\mathrm{sin}\theta\:=\:{n}\pi\:\mathrm{and}\:\mathrm{if}\:\mathrm{not},\:\mathrm{then} \\ $$$$\mathrm{1}\:+\:\frac{\mathrm{1}}{\mathrm{cos}\theta}\:=\:\mathrm{2cos}\theta \\ $$$$\Rightarrow\:\mathrm{1}\:+\:\mathrm{cos}\theta\:=\:\mathrm{2cos}^{\mathrm{2}} \theta \\ $$$$\Rightarrow\:\mathrm{cos}\theta\:=\:\mathrm{2cos}^{\mathrm{2}} \theta\:−\:\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{cos}\theta\:=\:\mathrm{cos2}\theta \\ $$$$\Rightarrow\:\theta\:=\:\mathrm{2}{n}\pi\:\pm\:\mathrm{2}\theta \\ $$$$\mathrm{3}\theta\:=\:\mathrm{2}{n}\pi\:\mathrm{or}\:−\theta\:=\:\mathrm{2}{n}\pi \\ $$$$\theta\:=\:\frac{\mathrm{2}{n}\pi}{\mathrm{3}}\:\mathrm{or}\:\theta\:=\:−\mathrm{2}{n}\pi. \\ $$$$\mathrm{I}\:\mathrm{do}\:\mathrm{not}\:\mathrm{get}\:\theta\:=\:\left(\mathrm{2}{n}\:+\:\mathrm{1}\right)\pi\:\pm\:\frac{\pi}{\mathrm{3}}.\:\mathrm{Why}? \\ $$
Commented by prakash jain last updated on 24/May/17
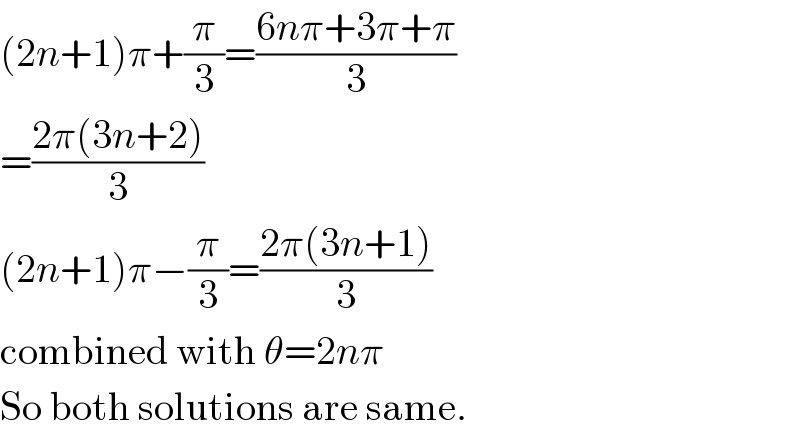
$$\left(\mathrm{2}{n}+\mathrm{1}\right)\pi+\frac{\pi}{\mathrm{3}}=\frac{\mathrm{6}{n}\pi+\mathrm{3}\pi+\pi}{\mathrm{3}} \\ $$$$=\frac{\mathrm{2}\pi\left(\mathrm{3}{n}+\mathrm{2}\right)}{\mathrm{3}} \\ $$$$\left(\mathrm{2}{n}+\mathrm{1}\right)\pi−\frac{\pi}{\mathrm{3}}=\frac{\mathrm{2}\pi\left(\mathrm{3}{n}+\mathrm{1}\right)}{\mathrm{3}} \\ $$$$\mathrm{combined}\:\mathrm{with}\:\theta=\mathrm{2}{n}\pi \\ $$$$\mathrm{So}\:\mathrm{both}\:\mathrm{solutions}\:\mathrm{are}\:\mathrm{same}. \\ $$
Commented by ajfour last updated on 24/May/17
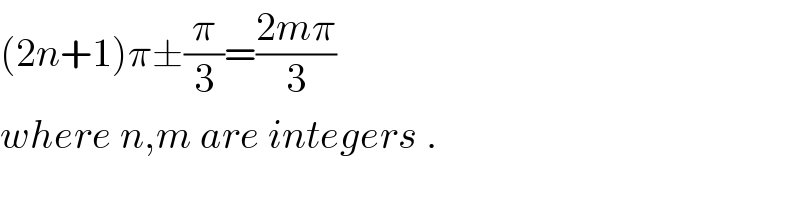
$$\left(\mathrm{2}{n}+\mathrm{1}\right)\pi\pm\frac{\pi}{\mathrm{3}}=\frac{\mathrm{2}{m}\pi}{\mathrm{3}} \\ $$$${where}\:{n},{m}\:{are}\:{integers}\:. \\ $$
Commented by Tinkutara last updated on 24/May/17

$$\mathrm{Thanks}. \\ $$
Commented by ajfour last updated on 24/May/17
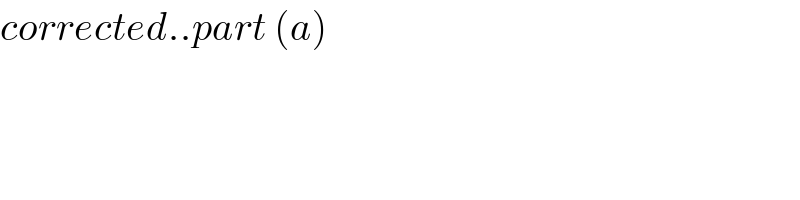
$${corrected}..{part}\:\left({a}\right) \\ $$
