
Question Number 138391 by ajfour last updated on 13/Apr/21
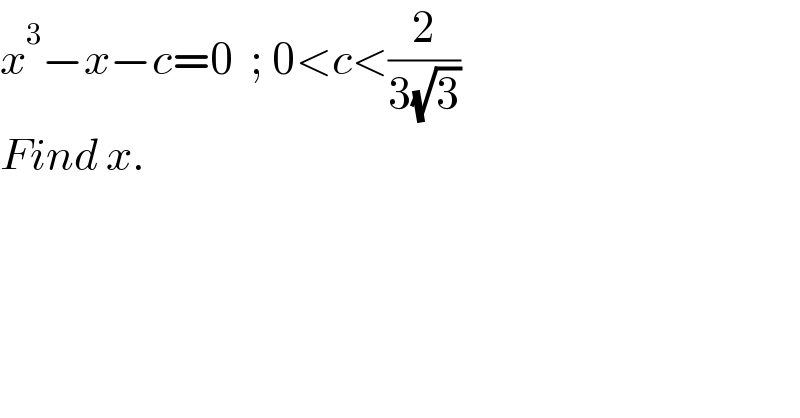
$${x}^{\mathrm{3}} −{x}−{c}=\mathrm{0}\:\:;\:\mathrm{0}<{c}<\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$ $${Find}\:{x}. \\ $$
Answered by ajfour last updated on 13/Apr/21
![let t^2 +pt+q=0 (x^3 −t^3 )−pt^2 −(x+qt)−c=0 let x−t=z (x−t){(x−t)^2 +3tx}−pt^2 −(x−t) +(q+1)t−c=0 z(z^2 +3tz+3t^2 )−z−{pt^2 −(q+1)t+c}=0 z^3 +3tz^2 +(3t^2 −1)z=pt^2 −(q+1)t+c let q=−1 pt^2 =−c & t^2 +pt−1=0 −(c/p)+pt−1=0 t=((p+c)/p^2 ) p(((p+c)/p^2 ))^2 =−c [p<0] cp^3 +p^2 +2cp+c^2 =0 p^3 +(p^2 /c)+2p+c=0 let p=s−(1/(3c)) s^3 −(s^2 /c)+(s/(3c^2 ))−(1/(27c^3 )) +(1/c)(s^2 −((2s)/(3c))+(1/(9c^2 )))+2s−(2/(3c))+c=0 ⇒ s^3 +(2−(1/(3c^2 )))s+(2/(27c^3 ))−(2/(3c))+c=0 D=((1/(27c^3 ))−(1/(3c))+(c/2))^2 −((1/(9c^2 ))−(2/3))^3 =(1/(9c^2 ))+(c^2 /4)−(2/(81c^4 ))−(1/3)+(1/(27c^2 )) +(8/(27))+(2/(81c^4 ))−(4/(27c^2 )) D=(c^2 /4)−(1/(27)) (same old tragedy..)](Q138392.png)
$${let}\:\:\:{t}^{\mathrm{2}} +{pt}+{q}=\mathrm{0} \\ $$ $$\left({x}^{\mathrm{3}} −{t}^{\mathrm{3}} \right)−{pt}^{\mathrm{2}} −\left({x}+{qt}\right)−{c}=\mathrm{0} \\ $$ $${let}\:\:{x}−{t}={z} \\ $$ $$\left({x}−{t}\right)\left\{\left({x}−{t}\right)^{\mathrm{2}} +\mathrm{3}{tx}\right\}−{pt}^{\mathrm{2}} −\left({x}−{t}\right) \\ $$ $$+\left({q}+\mathrm{1}\right){t}−{c}=\mathrm{0} \\ $$ $${z}\left({z}^{\mathrm{2}} +\mathrm{3}{tz}+\mathrm{3}{t}^{\mathrm{2}} \right)−{z}−\left\{{pt}^{\mathrm{2}} −\left({q}+\mathrm{1}\right){t}+{c}\right\}=\mathrm{0} \\ $$ $${z}^{\mathrm{3}} +\mathrm{3}{tz}^{\mathrm{2}} +\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{1}\right){z}={pt}^{\mathrm{2}} −\left({q}+\mathrm{1}\right){t}+{c} \\ $$ $${let}\:\:{q}=−\mathrm{1} \\ $$ $${pt}^{\mathrm{2}} =−{c} \\ $$ $$\&\:\:{t}^{\mathrm{2}} +{pt}−\mathrm{1}=\mathrm{0} \\ $$ $$−\frac{{c}}{{p}}+{pt}−\mathrm{1}=\mathrm{0} \\ $$ $${t}=\frac{{p}+{c}}{{p}^{\mathrm{2}} } \\ $$ $${p}\left(\frac{{p}+{c}}{{p}^{\mathrm{2}} }\right)^{\mathrm{2}} =−{c}\:\:\:\:\:\:\left[{p}<\mathrm{0}\right] \\ $$ $${cp}^{\mathrm{3}} +{p}^{\mathrm{2}} +\mathrm{2}{cp}+{c}^{\mathrm{2}} =\mathrm{0} \\ $$ $${p}^{\mathrm{3}} +\frac{{p}^{\mathrm{2}} }{{c}}+\mathrm{2}{p}+{c}=\mathrm{0} \\ $$ $${let}\:\:{p}={s}−\frac{\mathrm{1}}{\mathrm{3}{c}} \\ $$ $${s}^{\mathrm{3}} −\frac{{s}^{\mathrm{2}} }{{c}}+\frac{{s}}{\mathrm{3}{c}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{27}{c}^{\mathrm{3}} } \\ $$ $$+\frac{\mathrm{1}}{{c}}\left({s}^{\mathrm{2}} −\frac{\mathrm{2}{s}}{\mathrm{3}{c}}+\frac{\mathrm{1}}{\mathrm{9}{c}^{\mathrm{2}} }\right)+\mathrm{2}{s}−\frac{\mathrm{2}}{\mathrm{3}{c}}+{c}=\mathrm{0} \\ $$ $$\Rightarrow\:\:{s}^{\mathrm{3}} +\left(\mathrm{2}−\frac{\mathrm{1}}{\mathrm{3}{c}^{\mathrm{2}} }\right){s}+\frac{\mathrm{2}}{\mathrm{27}{c}^{\mathrm{3}} }−\frac{\mathrm{2}}{\mathrm{3}{c}}+{c}=\mathrm{0} \\ $$ $${D}=\left(\frac{\mathrm{1}}{\mathrm{27}{c}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{3}{c}}+\frac{{c}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\mathrm{9}{c}^{\mathrm{2}} }−\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{3}} \\ $$ $$\:\:=\frac{\mathrm{1}}{\mathrm{9}{c}^{\mathrm{2}} }+\frac{{c}^{\mathrm{2}} }{\mathrm{4}}−\frac{\mathrm{2}}{\mathrm{81}{c}^{\mathrm{4}} }−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{27}{c}^{\mathrm{2}} } \\ $$ $$\:\:+\frac{\mathrm{8}}{\mathrm{27}}+\frac{\mathrm{2}}{\mathrm{81}{c}^{\mathrm{4}} }−\frac{\mathrm{4}}{\mathrm{27}{c}^{\mathrm{2}} } \\ $$ $${D}=\frac{{c}^{\mathrm{2}} }{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{27}} \\ $$ $$\left({same}\:{old}\:{tragedy}..\right) \\ $$
