
Question Number 138153 by mathlove last updated on 10/Apr/21
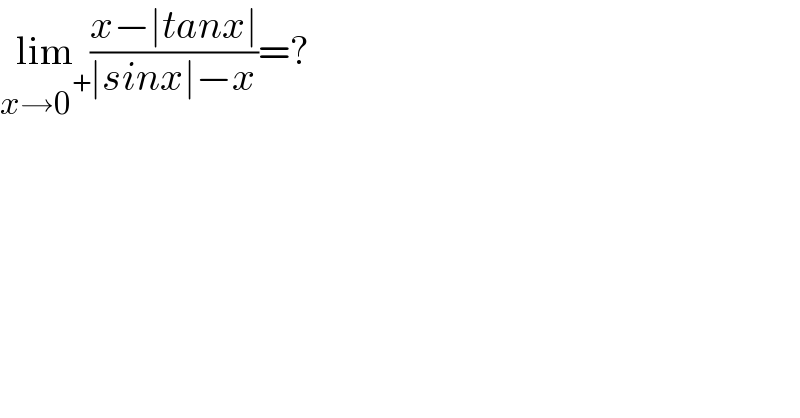
$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{{x}−\mid{tanx}\mid}{\mid{sinx}\mid−{x}}=? \\ $$
Answered by TheSupreme last updated on 10/Apr/21
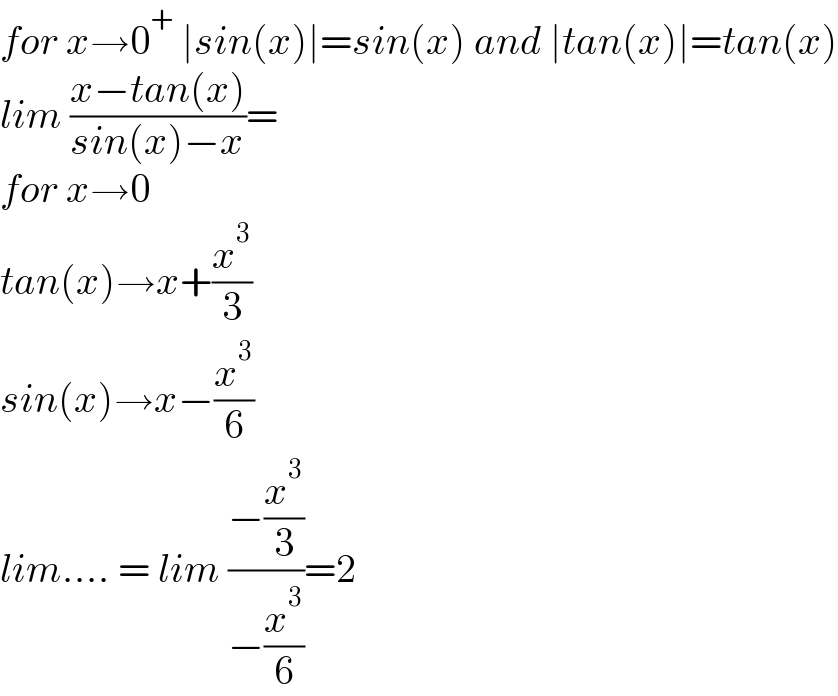
$${for}\:{x}\rightarrow\mathrm{0}^{+} \:\mid{sin}\left({x}\right)\mid={sin}\left({x}\right)\:{and}\:\mid{tan}\left({x}\right)\mid={tan}\left({x}\right) \\ $$$${lim}\:\frac{{x}−{tan}\left({x}\right)}{{sin}\left({x}\right)−{x}}= \\ $$$${for}\:{x}\rightarrow\mathrm{0} \\ $$$${tan}\left({x}\right)\rightarrow{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}} \\ $$$${sin}\left({x}\right)\rightarrow{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}} \\ $$$${lim}....\:=\:{lim}\:\frac{−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}}{−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}}=\mathrm{2} \\ $$
Commented by greg_ed last updated on 10/Apr/21
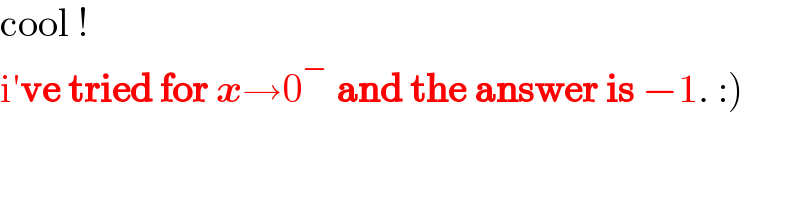
$$\mathrm{cool}\:! \\ $$$$\left.\mathrm{i}'\boldsymbol{\mathrm{ve}}\:\boldsymbol{\mathrm{tried}}\:\boldsymbol{\mathrm{for}}\:\boldsymbol{{x}}\rightarrow\mathrm{0}^{−} \:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{answer}}\:\boldsymbol{\mathrm{is}}\:−\mathrm{1}.\::\right) \\ $$
