
Previous in Relation and Functions Next in Relation and Functions
Question Number 13811 by Tinkutara last updated on 23/May/17
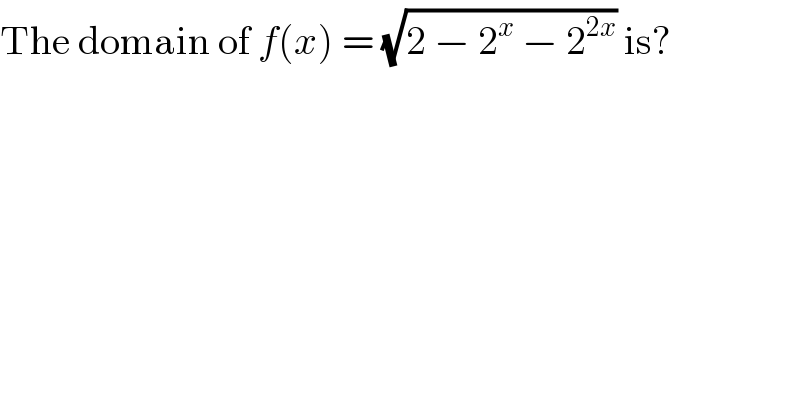
$$\mathrm{The}\:\mathrm{domain}\:\mathrm{of}\:{f}\left({x}\right)\:=\:\sqrt{\mathrm{2}\:−\:\mathrm{2}^{{x}} \:−\:\mathrm{2}^{\mathrm{2}{x}} }\:\mathrm{is}? \\ $$
Commented by RasheedSindhi last updated on 24/May/17

$$\mathrm{Sorry},\:\mathrm{wrong}\:\mathrm{process}. \\ $$
Answered by ajfour last updated on 23/May/17
![let 2^x =t >0 ....(i) ⇒ t^2 +t−2≤0 t^2 +2t−t−2≤0 (t−1)(t+2)≤0 ⇒ −2≤t≤1 ....(ii) from (i) and (ii), 0<t(=2^x )≤1 ⇒ x∈(−∞, 0] .](Q13813.png)
$${let}\:\mathrm{2}^{{x}} ={t}\:>\mathrm{0}\:\:\:\:....\left({i}\right) \\ $$$$\Rightarrow\:{t}^{\mathrm{2}} +{t}−\mathrm{2}\leqslant\mathrm{0} \\ $$$${t}^{\mathrm{2}} +\mathrm{2}{t}−{t}−\mathrm{2}\leqslant\mathrm{0} \\ $$$$\left({t}−\mathrm{1}\right)\left({t}+\mathrm{2}\right)\leqslant\mathrm{0} \\ $$$$\Rightarrow\:\:\:\:\:\:\:−\mathrm{2}\leqslant{t}\leqslant\mathrm{1}\:\:\:\:....\left({ii}\right) \\ $$$${from}\:\left({i}\right)\:{and}\:\left({ii}\right), \\ $$$$\mathrm{0}<{t}\left(=\mathrm{2}^{{x}} \right)\leqslant\mathrm{1} \\ $$$$\Rightarrow\:{x}\in\left(−\infty,\:\mathrm{0}\right]\:. \\ $$
Commented by Tinkutara last updated on 23/May/17

$$\mathrm{Thanks}. \\ $$
