
Question Number 13806 by ajfour last updated on 23/May/17
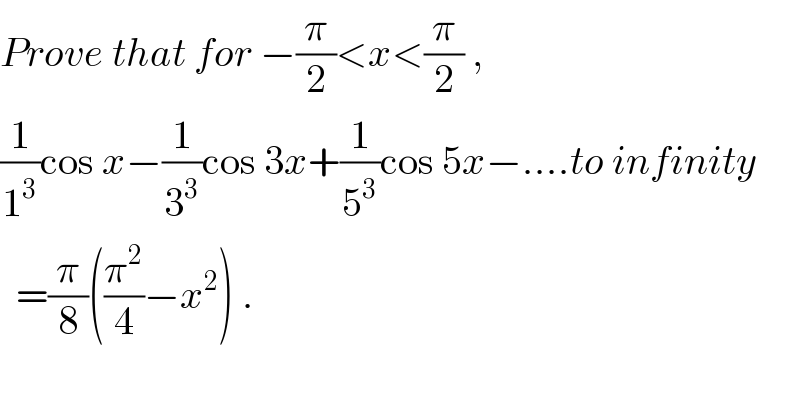
$${Prove}\:{that}\:{for}\:−\frac{\pi}{\mathrm{2}}<{x}<\frac{\pi}{\mathrm{2}}\:, \\ $$ $$\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{3}} }\mathrm{cos}\:{x}−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3}} }\mathrm{cos}\:\mathrm{3}{x}+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{3}} }\mathrm{cos}\:\mathrm{5}{x}−....{to}\:{infinity} \\ $$ $$\:\:=\frac{\pi}{\mathrm{8}}\left(\frac{\pi^{\mathrm{2}} }{\mathrm{4}}−{x}^{\mathrm{2}} \right)\:. \\ $$
Commented byprakash jain last updated on 24/May/17

$$\mathrm{LHS}\:\mathrm{looks}\:\mathrm{like}\:\mathrm{fourier}\:\mathrm{series} \\ $$ $$\mathrm{expansion}.\: \\ $$ $$\mathrm{I}\:\mathrm{will}\:\mathrm{look}\:\mathrm{for}\:\mathrm{appropriate}\:\mathrm{function} \\ $$ $$\mathrm{to}\:\mathrm{start}\:\mathrm{with}. \\ $$
