
Question Number 137899 by bemath last updated on 08/Apr/21
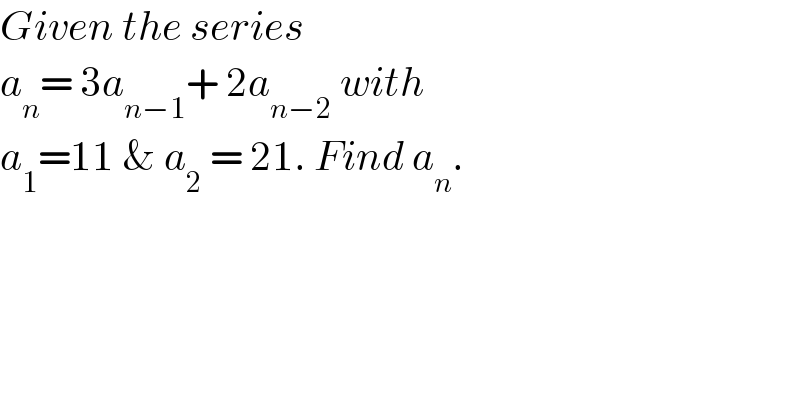
$${Given}\:{the}\:{series}\: \\ $$ $${a}_{{n}} =\:\mathrm{3}{a}_{{n}−\mathrm{1}} +\:\mathrm{2}{a}_{{n}−\mathrm{2}} \:{with}\: \\ $$ $${a}_{\mathrm{1}} =\mathrm{11}\:\&\:{a}_{\mathrm{2}} \:=\:\mathrm{21}.\:{Find}\:{a}_{{n}} . \\ $$
Answered by benjo_mathlover last updated on 08/Apr/21

$${characteristics}\:{equation} \\ $$ $${r}^{\mathrm{2}} −\mathrm{3}{r}−\mathrm{2}\:=\:\mathrm{0}\:;\:{r}=\frac{\mathrm{3}\pm\sqrt{\mathrm{17}}}{\mathrm{2}} \\ $$ $${a}_{{n}} \:=\:{A}.\left(\frac{\mathrm{3}+\sqrt{\mathrm{17}}}{\mathrm{2}}\right)^{{n}} +{B}\left(\frac{\mathrm{3}−\sqrt{\mathrm{17}}}{\mathrm{2}}\right)^{{n}} \\ $$ $${with}\:{n}=\mathrm{1}\Rightarrow\mathrm{11}\:=\:\frac{\mathrm{3}}{\mathrm{2}}\left({A}+{B}\right)+\frac{\sqrt{\mathrm{17}}}{\mathrm{2}}\left({A}−{B}\right) \\ $$ $${with}\:{n}=\mathrm{2}\Rightarrow\mathrm{21}=\frac{\mathrm{13}}{\mathrm{2}}\left({A}+{B}\right)+\frac{\mathrm{3}\sqrt{\mathrm{17}}}{\mathrm{2}}\left({A}−{B}\right) \\ $$ $${A}=\left(\frac{\mathrm{20}−\mathrm{3}\sqrt{\mathrm{17}}}{\:\sqrt{\mathrm{17}}\:}\right)\:;\:{B}=−\left(\frac{\mathrm{20}+\mathrm{3}\sqrt{\mathrm{17}}}{\:\sqrt{\mathrm{17}}}\right) \\ $$ $$\therefore\:{a}_{{n}} =\:\left(\frac{\mathrm{20}−\mathrm{3}\sqrt{\mathrm{17}}}{\:\sqrt{\mathrm{17}}}\right)\left(\frac{\mathrm{3}+\sqrt{\mathrm{17}}}{\mathrm{2}}\right)^{{n}} −\left(\frac{\mathrm{20}+\mathrm{3}\sqrt{\mathrm{17}}}{\:\sqrt{\mathrm{17}}}\right)\left(\frac{\mathrm{3}−\sqrt{\mathrm{17}}}{\mathrm{2}}\right)^{{n}} \\ $$
